e
ELEKTROTEHNIKA
plus
Glavna stran
Kazalo (osnovni nivo)
Kazalo (višji nivo)
Predstavitev projekta
Minimalne zahteve

3.2 Vezave upora, tuljave in kondenzatorja

3 Lastnost in zakonitosti izmeničnih krogov
 >> 

Iz e-ELEKTROTEHNIKA plus

Skoči na: navigacija, iskanje
Slika 3.2.2: Upornost sestavljenega izmeničnega kroga
Fotografija 47

V okviru enosmernih električnih krogov smo obravnavali kroge predvsem z upori in drugimi elementi z ohmsko upornostjo, kot so npr. grelniki in žarnice. Spoznali smo relativno enostavno odvisnost toka od napetosti in vezave uporov. V izmeničnem krogu, v katerem je poleg upora še tuljava ali kondenzator ali oba hkrati, pa je glede na vpliv, ki ga imata ta elementa v izmeničnem krogu (pogl. 3.1), pričakovati pestrejše dogajanje in tudi drugačno odvisnost toka.


Glede na to, da sta induktivna in kapacitivna upornost odvisni od frekvence in povzročata fazni premik med tokom in napetostjo, lahko za izmenični krog s poljubno vezavo upora, tuljave in/ali kondenzatorja na splošno sklepamo:


  • Poljubna vezava upora, tuljave in kondenzatorja v izmeničnem krogu povzroča na splošno med napetostjo in tokom izvora fazni premik (φ).
  • Tok, prevodnost oziroma upornost poljubne vezave upora, tuljave in kondenzatorja v izmeničnem krogu je odvisna od frekvence.


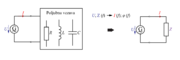
Upornost sestavljenega izmeničnega kroga (slika 3.2.2) ima torej širši pomen kot upornost sestavljenega enosmernega kroga. Zato jo tudi drugače imenujemo in označujemo:


  • Upornost izmeničnega kroga s poljubno vezavo upora, tuljave in (ali) kondenzatorja imenujemo impedanca[1], označujemo pa jo s črko Z.
  • Impedanco poljubne vezave upora, tuljave in (ali) kondenzatorja v izmeničnem krogu lahko določimo s kvocientom maksimalnih, lahko pa tudi bolj praktičnih, v praksi pogosto izmerjenih ali izračunanih efektivnih vrednosti napetosti in toka:



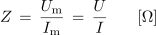
Enakovredno lahko računamo v sestavljenih izmeničnih krogih tudi s prevodnostjo vezav:


  • Prevodnost sestavljenega izmeničnega kroga imenujemo admitanca[2] , označujemo pa jo z veliko črko Y.
  • Admitanco vezave v izmeničnem krogu lahko določimo kot obratno vrednost impedance vezave:



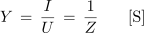
Pri vsem navedenem ne smemo spregledati:


  • Z, Y in φ imajo pomen, kot smo ga opisali, le pri sinusni obliki napetosti in toka.


Glede obravnave lastnosti izmeničnih krogov z različnimi vezavami navedenih elementov se pred obravnavo prve od takih vezav dogovorimo za pristop, ki bo veljal za večino podobnih primerov:


  • Fazne razmere v vezavi z uporom, tuljavo in/ali kondenzatorjem v izmeničnem krogu bomo v večini primerov zadovoljivo prikazali s kazalčnim diagramom.
  • Če kazalčni diagram rišemo le informativno, je tudi dolžina kazalcev informativna. Če pa s kazalčnim diagramom grafično rešujemo določeno nalogo, pred risanjem kazalčnega diagrama izberemo merilo za določitev dolžine kazalcev, npr. M: 4 V = 1 cm (štirim voltom ustreza 1 cm) ali 5 mA = 1 cm ...
  • Če bomo kazalčni diagram risali v povezavi s časovnim diagramom, bomo s kazalci v kazalčnem diagramu predstavili maksimalne vrednosti sinusnih količin (Um, Im).
  • Kadar bomo risali samo kazalčni diagram količin, katerih vrednosti bomo izmerili ali izračunali iz efektivnih vrednosti, trenutne vrednosti količin pa nas ne bodo zanimale, bomo dolžino kazalcev priredili efektivni vrednosti količin (Im⁄√2 …). Slika faznih razmer in računanje električnih količin se zaradi tega ne bo spremenilo.
  • Kazalčni diagram začnemo risati tako, da najprej na pozitivno vodoravno os koordinatnega sistema narišemo kazalec skupne količine elementov kroga.
  • Kazalce ostalih količin narišemo primerjalno s kazalcem skupne količine.
  • Pri risanju električnih krogov, katerih obravnava bo temeljila na izmerjenih, praviloma efektivnih ali izračunanih efektivnih vrednostih, bomo uporabili oznake za efektivne vrednosti. V primerih, ki bodo narekovali obravnavo električnega kroga s trenutnimi vrednostmi, pa bomo dosledno uporabili oznake za trenutne in maksimalne vrednosti (u, Um ... ).


Zaradi velike podobnosti obravnave različnih vezav upora tuljave in kondenzatorja bomo obravnavali predvsem tiste vezave, ki bodo prinašale nova spoznanja. To bo predvsem zaporedna vezava upora in tuljave in zaporedna vezava vseh treh elementov ter vzporedna vezava upora in kondenzatorja in vzporedna vezava vseh treh elementov. Na osnovi spoznanj pri obravnavi navedenih vezav bomo naloge v zvezi z zaporedno vezavo upora in kondenzatorja ter vzporedno vezavo upora in tuljave znali rešiti samostojno.


Značilnost časovnega poteka moči in energije ter računanje moči za poljubno vezavo upora, tuljave in kondenzatorja bomo na univerzalen način obravnavali na koncu tega poglavja.


Opombe

  1. ↑ tudi polna upornost
  2. ↑ tudi polna prevodnost


Podpoglavja:


3.1.3.4 Energija in moč v kapacitivnem izmeničnem krogu 3.2.1 Zaporedna vezava upora in tuljave
Vzpostavljeno iz »http://eele.fe.uni-lj.si/wiki/index.php/Vezave_upora,_tuljave_in_kondenzatorja«

Osebna orodja