Iz e-ELEKTROTEHNIKA plus
Preizkusi znanje
- Vnesi rezultat 460
Vnesi rezultat 46
Izračunaj tok skozi tuljavo vzporednega RLC vezja , če je tok skozi upor 3 A, skozi kondenzator pa 6A pri faznem kotu 60º oziroma -60º.2I60 =11.2AI-60 =0.8Aasdasfasd - Vnesi rezultat 470
Vnesi rezultat 47
Vzporedno so vezani upor z upornostjo 20 Ω, tuljava z upornostjo 20 Ω in kondenzator z upornostjo 50 Ω ter priključeni na napetost 110 V. Izračunaj impedanco in delovno moč.2Z =17ΩP =605Wasdasfasd - Vnesi rezultat 480
Vnesi rezultat 48
Kolikšen je faktor moči vzporednega RLC vezja (upor z upornostjo 20 Ω, tuljava z induktivno upornostjo 25 Ω, kondenzator s kapacitivno upornostjo 50 Ω), ki je priključeno na napetost 100 V?1cosφ =0.92asdasfasd - Vnesi rezultat 490
Vnesi rezultat 49
Izračunaj impedanco in tok vzporednega RLC vezja, katerega ohmska in induktivna upornost sta enaki 20 Ω, kapacitivna upornost pa 50 Ω, delovni tok pa 2 A.2Z =17ΩI =2.35Aasdasfasd - Vnesi rezultat 500
Vnesi rezultat 50
V vzporedni RLC vezavi poznamo: upor z upornostjo 25 Ω, tuljavo z upornostjo 40 Ω, kondenzator z upornostjo 20 Ω in napajalno napetost 100 V. Izračunaj vse tokove, fazni kot in impedanco.6IR =4AIL =2.5AIC =5AI =4.72Aφ =-32°Z =21Ωasdasfasd - Rešeni primer 300
Rešeni primer 30
Sinusna napetost 120 V napaja vzporedno vezavo, ki jo predstavljajo upor, tuljava in kondenzator. Tokovi, ki jih požene napetost po posameznih vejah, imajo naslednje vrednosti: 3 A skozi upor, 6 A skozi tuljavo in 2 A skozi kondenzator. Določi upornosti in prevodnosti posameznih elementov ter admitanco vezave.7Upornost ohmskega upora v vzporedni RLC vezavi je: R =40Ω.Tok v vsaki veji določa Ohmov zakon, ki povezuje napajalno napetost, upornost v veji in tok. Na tej osnovi tudi izračunamo upornosti elementov v posameznih vejah, pa tudi pripadajoče prevodnosti.
V prvem koraku poiščemo upornost in prevodnost upora.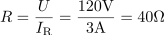 Prevodnost tega tega upora pa je: G =25mS.Tok v vsaki veji določa Ohmov zakon, ki povezuje napajalno napetost, upornost v veji in tok. Na tej osnovi tudi izračunamo upornosti elementov v posameznih vejah, pa tudi pripadajoče prevodnosti.
Prevodnost tega tega upora pa je: G =25mS.Tok v vsaki veji določa Ohmov zakon, ki povezuje napajalno napetost, upornost v veji in tok. Na tej osnovi tudi izračunamo upornosti elementov v posameznih vejah, pa tudi pripadajoče prevodnosti.
V prvem koraku poiščemo upornost in prevodnost upora.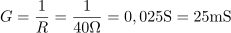 Induktivna upornost tuljave je: XL =20Ω.Tako kot smo izračunali upornost in prevodnost upora, določimo ta dva parametra tudi za tuljavo, saj poznamo efektivni tok skozi tuljavo pri znani napajalni napetosti.
Induktivna upornost tuljave je: XL =20Ω.Tako kot smo izračunali upornost in prevodnost upora, določimo ta dva parametra tudi za tuljavo, saj poznamo efektivni tok skozi tuljavo pri znani napajalni napetosti.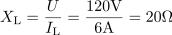 Tuljava ima induktivno prevodnost: BL =50mS.Tako kot smo izračunali upornost in prevodnost upora, določimo ta dva parametra tudi za tuljavo, saj poznamo efektivni tok skozi tuljavo pri znani napajalni napetosti.
Tuljava ima induktivno prevodnost: BL =50mS.Tako kot smo izračunali upornost in prevodnost upora, določimo ta dva parametra tudi za tuljavo, saj poznamo efektivni tok skozi tuljavo pri znani napajalni napetosti.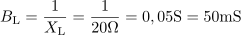 Kondenzator ima kapacitivno upornost: XC =60Ω.Postopek za izračun upornosti in prevodnosti kondenzatorja je enak postopku za izračun upornosti in prevodnosti tuljave.
Kondenzator ima kapacitivno upornost: XC =60Ω.Postopek za izračun upornosti in prevodnosti kondenzatorja je enak postopku za izračun upornosti in prevodnosti tuljave.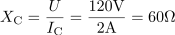 Kapacitivna prevodnost kondenzatorja pa je: BC =16.7mS.Postopek za izračun upornosti in prevodnosti kondenzatorja je enak postopku za izračun upornosti in prevodnosti tuljave.
Kapacitivna prevodnost kondenzatorja pa je: BC =16.7mS.Postopek za izračun upornosti in prevodnosti kondenzatorja je enak postopku za izračun upornosti in prevodnosti tuljave.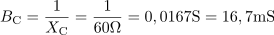 Admitanca vezja z vzporedno vezanimi elementi RLC znaša: Y =41.6mS.Admitanco vezja izračunamo kot geometrično vsoto prevodnosti posameznih elementov vezja.
Admitanca vezja z vzporedno vezanimi elementi RLC znaša: Y =41.6mS.Admitanco vezja izračunamo kot geometrično vsoto prevodnosti posameznih elementov vezja.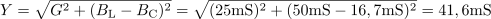 dasfasdfasdasdasfasd
dasfasdfasdasdasfasd - Rešeni primer 310
Rešeni primer 31
Vzporedno vezani elementi upor, tuljava in kondenzator so priključeni na napetost 40 V frekvence 200 Hz. Delovna moč je 40 W, induktivna jalova moč pa 20 var. Izračunaj upornost upora, induktivnost tuljave in kapacitivnost kondenzatorja, če je fazni kot -45 °.5Upornost upora, na katerem se sprošča delovna moč, je: R =40Ω.Izhajamo iz znane delovne moči in napetosti, kar nam omogoča izračun ohmske upornosti upora.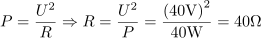 Induktivna upornost tuljave je: XL =80Ω.Tudi za izračun induktivne upornosti je pristop enak, saj poznamo induktivno jalovo moč in napetost. Na tej osnovi izračunamo induktivno upornost.
Induktivna upornost tuljave je: XL =80Ω.Tudi za izračun induktivne upornosti je pristop enak, saj poznamo induktivno jalovo moč in napetost. Na tej osnovi izračunamo induktivno upornost.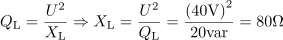 Tuljava, ki ima pri 200 Hz induktivno upornost 80 Ω, ima induktivnost: L =64mH.Ko poznamo induktivno upornost tuljave, je le še en korak do induktivnosti, saj poznamo tudi frekvenco, pri kateri ima tuljava tolikšno upornost.
Tuljava, ki ima pri 200 Hz induktivno upornost 80 Ω, ima induktivnost: L =64mH.Ko poznamo induktivno upornost tuljave, je le še en korak do induktivnosti, saj poznamo tudi frekvenco, pri kateri ima tuljava tolikšno upornost.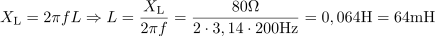 Kapacitivna prevodnost v vezju znaša: BC =37.5mS.Do kapacitivnosti kondenzatorja pridemo posredno, z izračunom kapacitivne prevodnosti BC ali pa tudi preko izračuna kapacitivne jalove moči QC.
Kapacitivna prevodnost v vezju znaša: BC =37.5mS.Do kapacitivnosti kondenzatorja pridemo posredno, z izračunom kapacitivne prevodnosti BC ali pa tudi preko izračuna kapacitivne jalove moči QC.
Tangens faznega kota povezuje jalovo prevodnost (BL – BC) in delovno prevodnost G, zato iz te povezave lahko izračunamo kapacitivno prevodnost BC.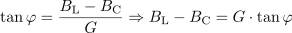
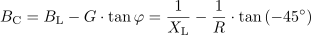
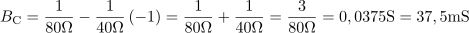 Kondenzator v vzporedni RLC vezavi ima kapacitivnost: C =29.9μF.Iz kapactivne prevodnosti pa pri znani frekvenci 200 Hz enostavno določimo kapacitivnost.
Kondenzator v vzporedni RLC vezavi ima kapacitivnost: C =29.9μF.Iz kapactivne prevodnosti pa pri znani frekvenci 200 Hz enostavno določimo kapacitivnost.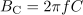
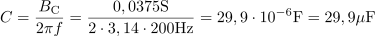 dasfasdfasdasdasfasd
dasfasdfasdasdasfasd
Poskus 2.2.4:
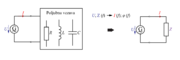
Vzporedno vezavo upora z upornostjo 750 Ω, tuljave z induktivnostjo 20 mH in kondenzatorja s kapacitivnostjo 0,1 µF priključimo na napetost 4,5 V/4,4 kHz (sl. 3.2.13)
Izmerimo efektivne toke IR, IL, IC in I ter preverimo izmerjeno z zakonom tokovnega vozlišča:
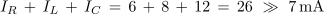
Aritmetična vsota efektivnih tokov je v danem primeru precej večja od efektivnega toka izvora. Nekaj podobnega smo ugotovili tudi pri zaporedni vezavi vseh treh elementov v poskusu 3.2.2, le da smo takrat imeli opravka z napetostmi.
Podpoglavja:
- 3.2.4.1 Kazalčni diagram napetosti in tokov
- 3.2.4.2 Trikotnik tokov in prevodnosti.
- 3.2.4.3 Vzporedna RLC vezava (interaktivna simulacija)
| | 3.2.4.1 Kazalčni diagram napetosti in tokov |