Iz e-ELEKTROTEHNIKA plus
| Vrstica 1: | Vrstica 1: | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
Matematične operacije (seštevanje, množenje ...) s kazalci električnih količin sinusnih oblik in enakih frekvenc, v izmeničnih krogih '''z zahtevnejšimi sestavljenimi vezavami''' lahko poenostavimo tako, da kazalce prenesemo v '''kompleksno ravnino''' in jih obravnavamo kot '''kompleksorje'''. | Matematične operacije (seštevanje, množenje ...) s kazalci električnih količin sinusnih oblik in enakih frekvenc, v izmeničnih krogih '''z zahtevnejšimi sestavljenimi vezavami''' lahko poenostavimo tako, da kazalce prenesemo v '''kompleksno ravnino''' in jih obravnavamo kot '''kompleksorje'''. | ||
| Vrstica 14: | Vrstica 5: | ||
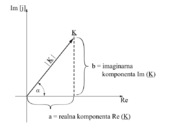
Slika 3.4.9: Kompleksor v kompleksni ravnini | Slika 3.4.9: Kompleksor v kompleksni ravnini | ||
| - | + | [[Image:eele_slika_3_4_9.svg|thumb|right|Slika 3.4.9: Kompleksor v kompleksni ravnini]] | |
<pomembno> | <pomembno> | ||
| Vrstica 86: | Vrstica 77: | ||
Slika 3.4.10: Grafični prikaz impedance v kompleksni ravnini | Slika 3.4.10: Grafični prikaz impedance v kompleksni ravnini | ||
| - | + | [[Image:eele_slika_3_4_10.svg|thumb|right|Slika 3.4.10: Grafični prikaz impedance v kompleksni ravnini]] | |
<pomembno> | <pomembno> | ||
| Vrstica 162: | Vrstica 153: | ||
Slika 3.4.12: Kompleksorja admitanc induktivnega in kapacitivnega značaja | Slika 3.4.12: Kompleksorja admitanc induktivnega in kapacitivnega značaja | ||
| - | + | [[Image:eele_slika_3_4_12.svg|thumb|right|Slika 3.4.12: Kompleksorja admitanc induktivnega in kapacitivnega značaja]] | |
<pomembno> | <pomembno> | ||
| Vrstica 198: | Vrstica 189: | ||
Slika 3.4.13 | Slika 3.4.13 | ||
| - | + | [[Image:eele_slika_3_4_13.svg|thumb|right|Slika 3.4.13]] | |
Potek računanja nakazujeta nadomestni vezavi b in c: | Potek računanja nakazujeta nadomestni vezavi b in c: | ||
| Vrstica 237: | Vrstica 228: | ||
Slika 3.4.14 | Slika 3.4.14 | ||
| - | + | [[Image:eele_slika_3_4_14.svg|thumb|right|Slika 3.4.14]] | |
Delne nadomestne impedance in admitance v kompleksni obliki: | Delne nadomestne impedance in admitance v kompleksni obliki: | ||
| Vrstica 285: | Vrstica 276: | ||
Slika 3.4.15 | Slika 3.4.15 | ||
| - | + | [[Image:eele_slika_3_4_15.svg|thumb|right|Slika 3.4.15]] | |
Na osnovi slike 3.4.15 lahko zapišemo kompleksor <u>''U''</u><sub>m</sub> v trigonometrični obliki, in sicer: | Na osnovi slike 3.4.15 lahko zapišemo kompleksor <u>''U''</u><sub>m</sub> v trigonometrični obliki, in sicer: | ||
| Vrstica 332: | Vrstica 323: | ||
Slika 3.4.16 | Slika 3.4.16 | ||
| - | + | [[Image:eele_slika_3_4_16.svg|thumb|right|Slika 3.4.16]] | |
Kompleksor impedance sestavljene vezave pretvorimo iz '''algebrske''' v '''eksponencialno''' obliko: | Kompleksor impedance sestavljene vezave pretvorimo iz '''algebrske''' v '''eksponencialno''' obliko: | ||
| Vrstica 405: | Vrstica 396: | ||
Slika 3.4.17 | Slika 3.4.17 | ||
| + | [[Image:eele_slika_3_4_17.svg|thumb|right|Slika 3.4.17]] | ||
</primer> | </primer> | ||
Redakcija: 09:56, 11. maj 2010
Matematične operacije (seštevanje, množenje ...) s kazalci električnih količin sinusnih oblik in enakih frekvenc, v izmeničnih krogih z zahtevnejšimi sestavljenimi vezavami lahko poenostavimo tako, da kazalce prenesemo v kompleksno ravnino in jih obravnavamo kot kompleksorje.
Ker je poljuben kompleksor (označimo ga z veliko podčrtano črko, npr. K, sl. 3.4.9) na splošno določen z realno (Re) in imaginamo (Im) komponento, električne količine pa so izključno realne količine, povejmo takoj na začetku:
Slika 3.4.9: Kompleksor v kompleksni ravnini
- Kompleksorji in kompleksni račun so le matematično orodje, ki poenostavlja računanje.
- Kompleksno obliko »nadenemo« sinusnim električnim količinam pred računanjem.
- Med računanjem z električnimi količinami v kompleksni obliki upoštevamo vsa pravila računanja s kompleksnimi števili, ko pa dobimo rezultat, kompleksno obliko praviloma opustimo.
Matematika ob robu:
<informacije>
Računanje v kompleksni ravnini
Večino problemov v splošni in tudi elektrotehniški praksi znamo rešiti z matematiko, ki temelji na realnih – predstavljivih številih, kot so npr. ± (1; 2; 36,8; π; 0,4; 2/3 ... ). V določenih primerih pa računi z realnimi števili obstanejo na problemu. kot je npr. kvadratni koren iz negativnega števila, za katerega med vso silno množico realnih števil ne najdemo rezultata. Matematiki so se pri tem zatekli k zvijači: ker √(-1) niso znali izračunati, so ga kot nekaj nepredstavljivega enostavno samo poimenovali z imaginarno[1] enoto in označili z »i«. V elektrotehniki bi oznako za imaginarno enoto lahko zamenjali z oznako za trenutno vrednost toka (i), zato v elektrotehniki uporabljamo za imaginarno enoto oznako »j«. Naloga npr. √(-4) je tako postala »rešljiva« na način √(-4) = √(4(-1)) = √4 √(-1) = 2j. Rezultata si sicer ne znamo predstavljati, toda pomembno je, kot bomo videli, da se z njim da računati.
Produktu imaginarne enote in poljubnega realnega števila, npr. 2j, pravimo imaginarno število.
Tako kot realna števila tvorijo horizontalno številsko premico oziroma realno os, po dogovoru domujejo imaginarna števila na vertikalni številski premici oziroma imaginarni osi. Obe osi določata ravnino, v kateri je poljubna točka določena z realno in imaginarno komponento.
Točki v ravnini, ki je določena z realno in imaginarno komponento, pravimo kompleksno število npr. Z, ravnini pa kompleksna ravnina. Kazalcu, ki določa kompleksno število s svojo dolžino in kotom s pozitivno realno osjo, pravimo kompleksor.
Splošni zapis kompleksnega števila oziroma kompleksorja:
SLIKE
Dolžina kazalca oziroma kompleksorja, ki določa kompleksno število, predstavlja absolutno vrednost kompleksnega števila:
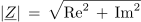
Kompleksnemu številu Z = a + jb zrcalnemu kompleksnemu številu z ozirom na realno os kompleksne ravnine, Z* = a - jb imenujemo konjugirano kompleksno število.
Pravila računanja s kompleksnimi števili v algebrski obliki
Seštevanje in odštevanje:
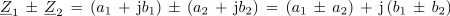
Množenje:
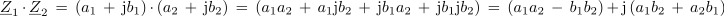
Zanimiv produkt:
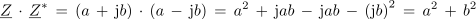
Pomembno: Produkt kompleksnega števila z njegovim konjugiranim kompleksnim številom je realno število!
Deljenje:
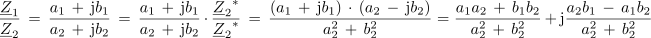
Zaradi enostavnejšega računanja je za operaciji množenja in deljenja ugodneje imeti kompleksna števila v eksponentni obliki:
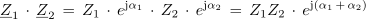
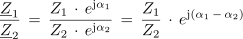
</informacije>
Računanje impedance in admitance v algebrski kompleksni obliki
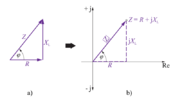
»Prehod« realnih električnih količin v algebrsko kompleksno obliko si oglejmo najprej na preprostih primerih impedance in admitance. Če trikotnik upornosti, npr. izmeničnega kroga z zaporedno vezavo upora in tuljave (sl. 3.4.10 a), prenesemo v kompleksno ravnino tako, kot kaže sl. 3.4.10 b, smo impedanci »nadeli« algebrsko kompleksno obliko.
Slika 3.4.10: Grafični prikaz impedance v kompleksni ravnini
- Kazalcu impedance Z priredimo v kompleksni ravnini kompleksor (Z), delovni komponenti R pozitivno realno komponento (R) kompleksorja Z ter jalovi induktivni komponenti XL impedance Z pozitivno imaginarno komponento (+ jXL) kompleksorja Z.
Algebrski zapis impedance zaporedne vezave upora in tuljave ima torej v kompleksni ravnini obliko:

oziroma
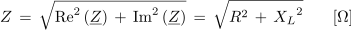
Impedanco izmeničnega kroga z zaporedno vezavo upora z upornostjo 20 Ω in tuljave z induktivno 30 Ω zapišemo potem v kompleksni obliki na način:
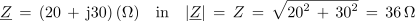
Fazni kot zaporedne vezave izračunamo v kompleksni obliki na osnovi imaginarne in realne komponente kompleksorja impedance ali admitance:
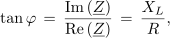
kar je že znana zgodba.
Podobno bi lahko naredili z impedanco kapacitivnega značaja, kompleksor impedance pa bi imel negativno imaginarno komponento (- jXC).
- Induktivna jalova komponenta XL impedance Z ima v kompleksni ravnini značaj pozitivne imaginarne komponente (jXL) kompleksorja Z.
- Kapacitivna jalova komponenta XC impedance Z ima v kompleksni ravnini značaj negativne imaginarne komponente (- jXC) kompleksorja Z.
Algebrski zapis impedance kapacitivnega značaja ima torej v kompleksni ravnini obliko:
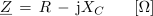
Impedanco izmeničnega kroga z zaporedno vezavo upora z upornostjo 40 Ω in kondenzatorja s kapacitivno upornostjo 50 Ω zapišemo potem v obliki:
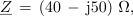
njena absolutna vrednost pa je
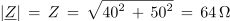
Vidimo, da se zapisa impedanc induktivnega in kapacitivnega značaja v kompleksni obliki razlikujeta v predznakih imaginarnih komponent. Ta ugotovitev je pomembna tudi za določitev značaja impedance ter delovne in jalove upornosti iz rezultata reševanja naloge sestavljene vezave.
- Pozitivni predznak imaginarne komponente (+ jX) kompleksorja impedance Z določa induktivni značaj impedance Z in pozitivni predznak faznega kota φ.
- Negativni predznak imaginarne komponente (- jX) kompleksorja impedance Z določa kapacitivni značaj impedance Z in negativni predznak faznega kota φ.
Kompleksni obliki zapisov admitanc induktivnega in kapacitivnega značaja dobimo na podoben način na osnovi trikotnikov admitanc (slika 3.4.12):
Slika 3.4.12: Kompleksorja admitanc induktivnega in kapacitivnega značaja
- Kazalcu admitance Y priredimo v kompleksni ravnini kompleksor Y.
- Delovni komponenti G admitance Y priredimo v kompleksni ravnini pozitivno realno komponento (G), induktivni jalovi komponenti BL negativno imaginarno komponento (- jBL) in kapacitivni jalovi komponenti BC admitance Y pozitivno (+ jBC) kompleksorja Y.
Algebrska zapisa admitanc induktivnega in kapacitivnega značaja imata torej v kompleksni ravnini obliko:
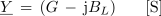
in
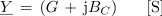
Admitanca Y je v kompleksni ravnini določena z absolutno vrednostjo |Y| kompleksorja admitance Y.
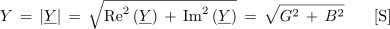
Fazni kot vzporedne vezave izračunamo na osnovi imaginarne in realne komponente na podoben način, kot smo to ugotovili za primer impedance.
Iz slike 3.4.12 in dobljenih izrazov za admitanco Y ugotavljamo, da ima predznak imaginarne komponente kompleksorja admitance nasproten pomen kot predznak imaginarne komponente kompleksorja impedance.
Primera:
Primer:
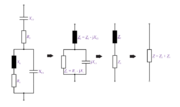
1. Izračunaj impedanco in fazni kot vezave upornosti, ki jo prikazuje slika 3.4.13 a. Upornost upora je 2 Ω, kapacitivna upornost je 4 Ω in induktivna upornost je 1Ω.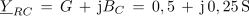
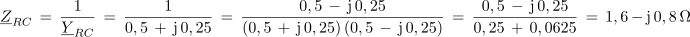
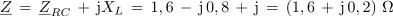
Iz izračunane impedance vezave v kompleksni obliki ugotavljamo: 1. Impedanca ima zaradi pozitivnega predznaka imaginarne komponente, induktivni značaj.2. Upornost delovne komponente impedance je 1,6 Ω, upornost jalove komponente pa 0,2 Ω. 3. Sestavljeno vezavo upornosti na sliki 3.4.13 a. bi lahko glede izvora enakovredno nadomestili z zaporedno vezavo upora z upornostjo 1,6 Ω in tuljave z induktivno upornostjo 0,2 Ω. Impedanca vezave:
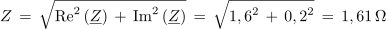
Fazni kot vezave:
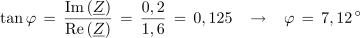
Primer:
2. Izračunaj impedanco in fazni kot sestavljene vezave upornosti, ki jo prikazuje slika 3.4.14 (R1 = 3 Ω, XL = 4 Ω, XC1 = 4 Ω, R2 = 2 Ω in XC2 = 4 Ω).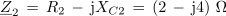
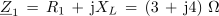
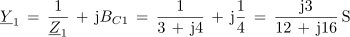
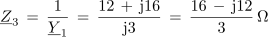
Impedanca celotne vezave v kompleksni obliki je po tem:
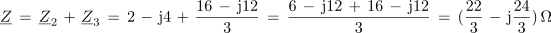
Impedanca vezave ima kapacitivni značaj (- j). Glede obremenitve izvora bi jo lahko nadomestili z zaporedno vezavo upora z upornostjo 22/3 Ω in kondenzatorja s kapacitivno upornostjo 24/3 Ω. Fazni kot vezave:
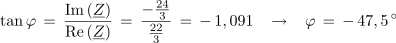
Računanje sinusnih napetosti in tokov v eksponentni kompleksni obliki
Algebrska oblika zapisa kompleksorjev električnih količin izmeničnih krogov ima to prednost, da sta iz nje neposredno razvidni delovna in jalova komponenta impedance, prevodnosti, toka ... in značaj jalovih komponent (induktivni, kapacitivni). Omogoča tudi preprosto seštevanje in odštevanje kazalcev količin sestavljenih izmeničnih krogov.
Algebrska oblika zapisa kompleksorjev električnih količin je zelo primerna za računanje impedanc in prevodnosti pa tudi napetosti in tokov na osnovi zakonov napetostnih zank in tokovnih vozlišč.
Pri uporabi Ohmovega zakona in računanju moči pa imamo opravka z operacijama množenja in deljenja. Čeprav je tudi v tem primeru možno računati s kompleksorji v algebrski obliki, pa je računanje preprostejše, če uporabimo eksponentno obliko zapisa kompleksorjev toka in napetosti.
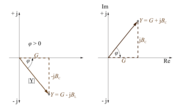
Najprej si kompleksor sinusne izmenične količine oglejmo nekoliko podrobneje. Dobimo ga, če kazalec npr. napetosti (slika 3.4.15 a) prenesemo v kompleksno ravnino (slika 3.4.15 b):
Slika 3.4.15
Na osnovi slike 3.4.15 lahko zapišemo kompleksor Um v trigonometrični obliki, in sicer:
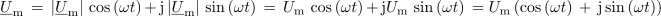
Če namesto trigonometričnega dela uporabimo enakovredni eksponentni operator ej(ωt) [2], dobimo eksponentno obliko zapisa kompleksorja sinusne napetosti:
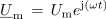
Podobno bi lahko naredili s kazalci maksimalnih vrednosti drugih izmeničnih količin. Iz praktičnih razlogov bomo v nadaljevanju, če ne bo drugače zahtevano, namesto z maksimalnimi, računali z efektivnimi vrednostmi izmeničnih količin.
Pri enakih frekvencah napetosti in toka kazalca le-teh v medsebojnem odnosu »mirujeta«, zato lahko kroženje kazalcev »spregledamo« (ωt = 0), tako kot tudi nismo upoštevali začetnih kotov. Če upoštevamo, da po dogovoru postavljamo kazalec oziroma kompleksor napetosti izvora na pozitivno realno os (kot če bi izbrali αu = 0), položaj kompleksorja zaostajajočega toka pa je s tem določen z negativnim kotom φ, dobimo za računanje obliko:
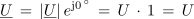
oziroma
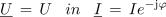
Ker sta v Ohmovem zakonu soudeleženi tudi impedanca in prevodnost, zapišimo v eksponentni obliki tudi kompleksorja teh dveh količin:
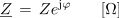
in
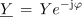
Eksponentna oblika zapisa kompleksorjev električnih količin izmeničnih krogov ima to prednost, da omogoča preprosto množenje in deljenje kazalcev količin sestavljenih izmeničnih krogov, iz rezultatov računanja pa so neposredno razvidne impedance in admitance, maksimalne ali efektivne vrednosti napetosti in tokov ter fazni kot in iz njegovega predznaka značaj jalovih komponent računanih količin.
Primera:
Primer:
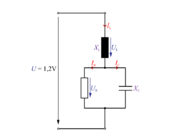
1. Med priključnima sponkama vezave na strani 6 je izmenična napetost 1,2 V (slika 3.4.16). Izračunaj toke elementov, napetosti na elementih ter fazni kot med kazalcema napetosti na tuljavi in kondenzatorju.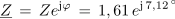
Tok skozi tuljavo je tok izvora:
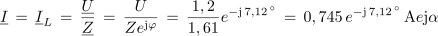
[3]Iz rezultata razberemo, da je efektivna vrednost toka izvora in tuljave 0,745 A in da tok zaostaja za napetostjo izvora za 7,12 °. Račun je res kratek in enostaven.Kompleksor induktivne upornosti jXL prevedemo iz algebrske oblike v eksponentno:
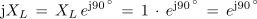
Napetost na tuljavi je potem:
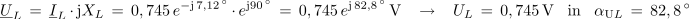
Kompleksor impedance ZRC prevedemo v eksponentno obliko:
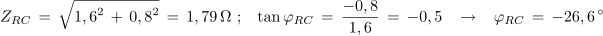
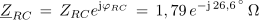
Napetost na uporu in kondenzatorju je:
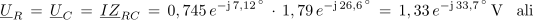
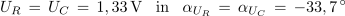
Ker je kazalec napetosti UL za 82,8 º pred kazalcem napetosti izvora (ki leži v vodoravni osi), kazalec napetosti UC pa za kazalcem U zaostaja za 33,7 º, je kot med njima vsota obeh kotov, torej 116,5 º.Tok skozi upor:
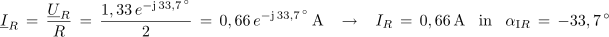
Tok skozi kondenzator:
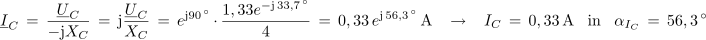
Geometrična vsota tokov IR in IC mora biti seveda enaka toku IL. Ker sta toka IR in IC med seboj pravokotna, lahko to preverimo s Pitagorovim izrekom (upoštevaj zanemarjena decimalna mest
a). Iz znanih kompleksnih vrednosti tokov in napetosti je za podano vezavo zelo preprosto določiti kazalčni diagram. Izberemo le merilo toka in napetosti ter kazalce vrišemo pod danimi koti.
Primer:
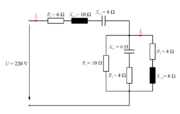
2. Izračunaj tok skozi tuljavo L4 in njegov fazni kot v izmeničnem krogu, ki ga prikazuje slika 3.4.17
Računanje moči sinusnega toka v eksponentni kompleksni obliki
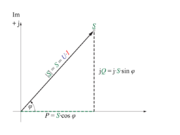
Če trikotnik moči poljubne vezave upora, tuljave in/ali kondenzatorja narišemo v kompleksno ravnino (slika 3.4.18), lahko ugotovimo:
Slika 3.4.18: Trikotnik moči v kompleksni ravnini
- Navidezno moč izmeničnega toka je v kompleksni ravnini ponazorjena s kompleksorjem S, katerega realna komponenta je delovna moč P, imaginarna komponenta pa jalova moč jQ.
Jalova moč ima lahko pri tem induktivni (jQL) ali kapacitivni (- jQC) značaj. V algebrski obliki zapišemo kompleksor moči S:
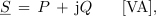
v eksponentni obliki pa
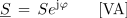
Pri računanju moči v eksponentni kompleksni obliki pa moramo biti previdni. Poglejmo:
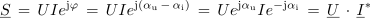
ali
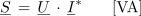
- Kompleksor moči S izmeničnega toka je določen s produktom kompleksorja napetosti U in konjugiranega kompleksorja toka I*.
Problem bi sicer lahko pričakovali, saj v istem kazalčnem diagramu lahko enakovredno obravnavamo le sinusne količine enakih frekvenc. Obravnavana navidezna moč pa je sestavljena iz delovne in izmenične jalove komponente, ki ima dvojno frekvenco toka oziroma napetosti.
Če upoštevamo še Ohmov zakon, ki velja tudi v kompleksni obliki U = I • Z, lahko izmenično moč računamo tudi v obliki:
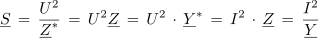
Primera:
Primer:
1. Izračunaj navidezno, delovno in jalovo moč izmeničnega toka pri podatkih U = 230 V, αU = 78 º, I = 2 A in αI = 48 º.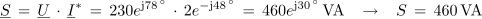
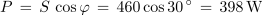
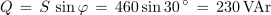
Primer:
2. Izračunaj navidezno delovno in jalovo moč izmeničnega toka v vezavi iz prvega primera tega poglavja (U = 1,2 • ej0º V, I = 0,745 • e-j7,12º A).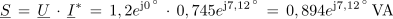
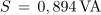
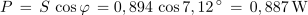
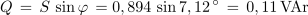
V sestavljenem izmeničnem krogu na splošno velja:
- Kompleksna moč večjega števila porabnikov je enaka vsoti kompleksnih moči posameznih porabnikov ne glede na vezavo le-teh.
Opombe
- ↑ imaginarius, lat. = le v mislih, domišljiji obstoječ, izmišljen, neresničen ...
- ↑
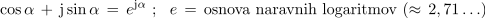
- ↑ Množenje kompleksorja z operatorjem ejα povzroča v kompleksni ravnini zasuk kompleksorja za kot α
Podpoglavja:
- 4.1.2.1 Računanje impedance in admitance v algebrski kompleksni obliki
- 4.1.2.2 Računanje sinusnih napetosti in tokov v eksponentni kompleksni obliki
- 4.1.2.3 Računanje moči sinusnega toka v eksponentni kompleksni obliki
| | 4.1.2.1 Računanje impedance in admitance v algebrski kompleksni obliki |