4.1.2 Računanje električnih količin v kompleksi ravnini

Iz e-ELEKTROTEHNIKA plus

Matematične operacije (seštevanje, množenje ...) s kazalci električnih količin sinusnih oblik in enakih frekvenc, v izmeničnih krogih z zahtevnejšimi sestavljenimi vezavami lahko poenostavimo tako, da kazalce prenesemo v kompleksno ravnino in jih obravnavamo kot kompleksorje.

Ker je poljuben kompleksor (označimo ga z veliko podčrtano črko, npr. K, sl. 3.4.9) na splošno določen z realno (Re) in imaginamo (Im) komponento, električne količine pa so izključno realne količine, povejmo takoj na začetku:

Matematika ob robu: <informacije> Računanje v kompleksni ravnini

Večino problemov v splošni in tudi elektrotehniški praksi znamo rešiti z matematiko, ki temelji na realnih – predstavljivih številih, kot so npr. ± (1; 2; 36,8; π; 0,4; 2/3 ... ). V določenih primerih pa računi z realnimi števili obstanejo na problemu. kot je npr. kvadratni koren iz negativnega števila, za katerega med vso silno množico realnih števil ne najdemo rezultata. Matematiki so se pri tem zatekli k zvijači: ker √(-1) niso znali izračunati, so ga kot nekaj nepredstavljivega enostavno samo poimenovali z imaginarno^[1] enoto in označili z »i«. V elektrotehniki bi oznako za imaginarno enoto lahko zamenjali z oznako za trenutno vrednost toka (i), zato v elektrotehniki uporabljamo za imaginarno enoto oznako »j«. Naloga npr. √(-4) je tako postala »rešljiva« na način √(-4) = √(4(-1)) = √4 √(-1) = 2j. Rezultata si sicer ne znamo predstavljati, toda pomembno je, kot bomo videli, da se z njim da računati.

Produktu imaginarne enote in poljubnega realnega števila, npr. 2j, pravimo imaginarno število.

Tako kot realna števila tvorijo horizontalno številsko premico oziroma realno os, po dogovoru domujejo imaginarna števila na vertikalni številski premici oziroma imaginarni osi. Obe osi določata ravnino, v kateri je poljubna točka določena z realno in imaginarno komponento.

Točki v ravnini, ki je določena z realno in imaginarno komponento, pravimo kompleksno število npr. Z, ravnini pa kompleksna ravnina. Kazalcu, ki določa kompleksno število s svojo dolžino in kotom s pozitivno realno osjo, pravimo kompleksor.

Splošni zapis kompleksnega števila oziroma kompleksorja:

SLIKE

Dolžina kazalca oziroma kompleksorja, ki določa kompleksno število, predstavlja absolutno vrednost kompleksnega števila:

Kompleksnemu številu zrcalnemu kompleksnemu številu z ozirom na realno os kompleksne ravnine, imenujemo konjugirano kompleksno število.

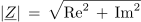
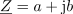
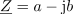
Pravila računanja s kompleksnimi števili v algebrski obliki

Seštevanje in odštevanje:

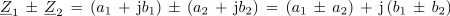
Množenje:

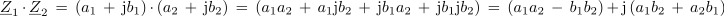
Zanimiv produkt:

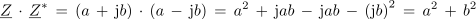
Pomembno: Produkt kompleksnega števila z njegovim konjugiranim kompleksnim številom je realno število!

Deljenje:

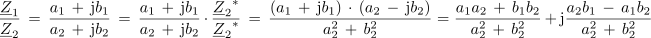
Zaradi enostavnejšega računanja je za operaciji množenja in deljenja ugodneje imeti kompleksna števila v eksponentni obliki:

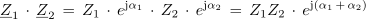
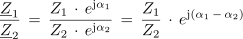
</informacije>

Opombe

1. ↑ imaginarius, lat. = le v mislih, domišljiji obstoječ, izmišljen, neresničen ...

Podpoglavja:

• 4.1.2.1 Računanje impedance in admitance v algebrski kompleksni obliki
• 4.1.2.2 Računanje sinusnih napetosti in tokov v eksponentni kompleksni obliki
• 4.1.2.3 Računanje moči sinusnega toka v eksponentni kompleksni obliki

4.1.1 Računanje na osnovi pravil reševanja trikotnikov

4.1.2.1 Računanje impedance in admitance v algebrski kompleksni obliki