Iz e-ELEKTROTEHNIKA plus
![](javascript: loadPicture("Eele_slika_7_3_7.svg", 1238);)
![](javascript: loadPicture("Eele_slika_7_3_8.svg", 1288);)
Iz oblike frekvenčnega poteka (karakteristike) toka lahko razberemo še eno, v bistvu najpomembnejšo lastnost zaporednega nihajnega kroga:
- Zaporedni nihajni krog prepušča zelo dobro tok resonančne frekvence in frekvenc, ki so resonančni blizu, toke višjih in nižjih frekvenc pa močno duši.
Če bi namesto izvora čiste sinusne napetosti na nihajni krog priključili izvor iz množice napetosti različnih frekvenc sestavljene napetosti, bi v nihajnem krogu imeli predvsem tok resonančne frekvence in toke, katerih frekvence so blizu resonančni.
- Zaporedni nihajni krog je pasovno prepustni frekvenčni filter.
- Lastnost nihajnega kroga, da iz množice tokov različnih frekvenc »izbira« in prepušča toke le določenih frekvenc, imenujemo selektivnost[1].
- Čim ožja je frekvenčna karakteristika in čim strmejši so njeni boki, tem večja je selektivnosti zaporednega nihajnega kroga.
Pravkar ugotovljena lastnost nihajnega kroga omogoča radijskim in TV sprejemnikom, da iz množice signalov, ki jih sprejema antena, izločijo le želenega. Sprejemniki z boljšo selektivnostjo bolje ločijo želeni signal od neželenega (ki ga ne želimo poslušati).
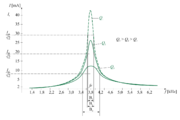
- Področje frekvenc, katerih toke zaporedni nihajni krog dobro prevaja, imenujemo prepustni frekvenčni pas nihajnega kroga (B)[2] (slika 7.3.7).
Bolj točno je prepustni frekvenčni pas zaporednega nihajnega kroga določen na naslednji način:
- Prepustni frekvenčni pas zaporednega nihajnega kroga je območje frekvenc, v katerem moč v nihajnem krogu ne pade pod Pr ⁄ 2 oziroma tok v nihajnem krogu ni manjši od Ir ⁄ √2.
- Širina prepustnega frekvenčnega pasu B je določena z razliko mejnih frekvenc prepustnega frekvenčnega pasu fmzg in fmsp.
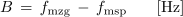
Enačbo za neposredno računanje širine frekvenčnega pasu B dobimo iz razmerja tokov pri resonančni in mejni frekvenci. Pot do enačbe je nekoliko zahtevnejša, zato napišimo le rezultat:
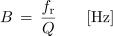
- Širina prepustnega frekvenčnega pasu zaporednega nihajnega kroga je premo sorazmerna z resonančno frekvenco in obratno sorazmerna s faktorjem kakovosti nihajnega kroga.
Oblika frekvenčne karakteristike ni ravno simetrična glede na resonančno frekvenco, toda za faktor kakovosti Q > 10 velja, da je prepustni pas glede na resonančno frekvenco praktično simetričen.
Primer:
Izračunaj širino frekvenčnega prepustnega pasu B, mejni frekvenci f1 in f2 ter toke pri resonančni in mejnih frekvencah za nihajni krog iz poskusa 7.3.1 (fr = 3768 Hz, Rt = 23 Ω).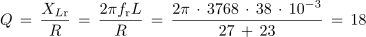
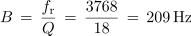
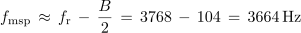
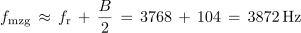
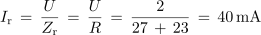
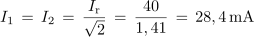
Pred naslednjim poskusom izračunajmo faktorje kakovosti nihajnega kroga iz poskusa 7.3.1 še pri upornosti upora 56 Ω in 150 Ω. V obeh primerih upoštevajmo ohmsko upornost tuljave (Rt = 23 Ω).
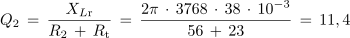
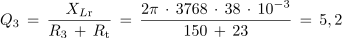
- Z naraščajočo delovno upornostjo kakovost nihajnega kroga pada.
Poskus 7.3.2:
Ponovimo poskus 7.3.1 tako, da namesto upora z upornostjo 27 Ω vključimo v krog najprej upor z upornostjo 56 Ω in potem še upor z upornostjo 150 Ω, torej tako, da pri stalni napetosti in frekvenci zmanjšujemo kakovost nihajnega kroga. Rezultat meritev prikazuje grafično slika 7.3.8.
- Večja ohmska upornost povzroči manjši resonančni tok in širši prepustni pas nihajnega kroga.
- Čim večja je kakovost nihajnega kroga, tem večji je resonančni tok, tem ožji je frekvenčni prepustni pas in tem boljša je selektivnost zaporednega nihajnega kroga.
Opombe
 7.3.1.2 Kakovost zaporednega nihajnega kroga
| 7.3.1.4 Frekvenčna karakteristika impedance zaporednega nihajnega kroga
|
