Iz e-ELEKTROTEHNIKA plus
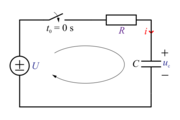
Polnilno vezje oblikujejo napetostni vir, stikalo, upor in kondenzator (slika 95). Kondenzator naj bo pred vklopom stikala, ob t0 = 0 s, prazen, da je uC(-0) = 0 V. Takoj za tem se v zanki pojavi tok, ki je prvi hip največji, i = U / R, saj je kondenzator še prazen. Po zelo kratkem času se le-ta delno naelektri in doseže napetost uC, zaradi česar se tok že rahlo zmanjša, i = (U - uC) / R. Tok očitno usiha, napetost kondenzatorja pa raste, vendar dlje kot do U ne pride. Ko polnilni tok povsem presahne, je kondenzator dokončno naelektren.
Povedano prelevimo v enačbe. Napišimo zančno enačbo za trenutek t > t0 in izrazimo napetost na uporu ter polnilni tok:
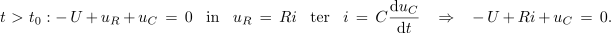
Odvajajmo napetostno enačbo (odvod napetosti U enosmernega vira je enak nič, odvod toka je di / dt in odvod napetosti kondenzatorja je duC / dt):
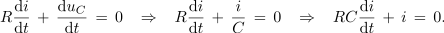
Produkt RC dimenzijsko ustreza sekundi, označimo ga s τ in nadaljujmo:
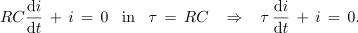
Enačba sporoča, da je tok funkcija, katere odvod je sorazmeren njej sami. To lastnost pa ima le eksponentna funkcija. Najdemo jo v eksponentni funkciji, multiplicirani s konstanto:
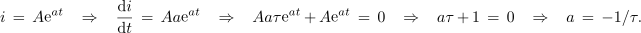
Eksponent funkcije je določen, manjka le še konstanta. Kondenzator je tik po vklopu še prazen. Iz zančne enačbe sledi začetna vrednost polnilnega toka,
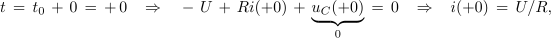
ki določa tudi iskano konstanto:
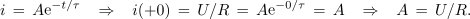
Rešitev je tu. Tok določa usihajoča časovna funkcija:
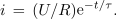
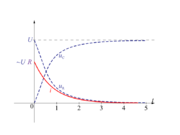
Ob vklopu stikala tok naraste na vrednost U / R, od tam dalje pa eksponentno usiha. Ob času t1 = τ je vrednost polnilnega toka (U / R) e-1 &kong; 0,3678 (U / R) oziroma 37 % začetnega toka, ob času t2 = 2τ še (U / R) e-2 = 0,1353 (U / R) oziroma 14 % začetnega toka, v času t3 = 3τ le še 5 % začetnega toka, v času t4 = 4τ komaj še 1,8 % začetnega toka in v času t5 = 5τ le še neznatnih 0,7 % začetnega toka. Konstanta τ določa torej dinamiko usihanja toka, imenujemo jo časovna konstanta vezja ali kar RC konstanta[1]. Čeravno je prehodno stanje vezja teoretično »neskončno dolgo«, se za čas prehodnega pojava smatra čas petih časovnih konstant; to je čas, ko se dinamika pojava umakne v zadnji %.
Iz toka i sledita še napetosti na uporu in kondenzatorju (slika 96):
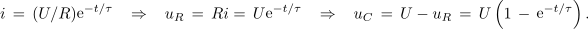
Dinamika napetosti na uporu je enaka opisani za tok, medtem ko je dinamika napetosti na kondenzatorju obratna. V času prve časovne konstante pridobi kondenzator 63 % končne napetosti, v času dveh že 86 % ... in v času 5τ že 99,3 % končne napetosti U. Sproti se v njem kopiči tudi energija:
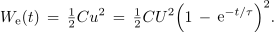
V času prve časovne konstante je v kondenzatorju 40 % končne energije, v času dveh časovnih konstant naraste na 75 % in v petih časovnih konstantah doseže praktično 99 % končne energije. Med polnjenjem kondenzatorja se v uporu sprošča toplota z močjo Ri2:
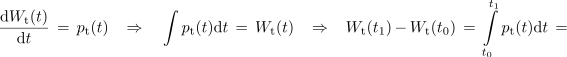
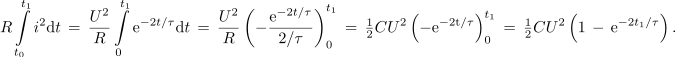
Pridobljena funkcija pove, koliko toplote se sprosti v uporu do časa t1. Ko bo t1 nekajkratnik τ, bo toplota dosegla vrednost, ki je enaka končni akumulirani energiji v kondenzatorju, torej CU2 / 2. Sporočilo? Med prehodnim pojavom se delo vira do polovice prelevi v energijo polja v kondenzatorju, do polovice pa v toploto v uporu (ne glede na upornost R); izkoristek polnjenja je 50 %.
Zgled 1
Z virom enosmerne napetosti 500 V želimo naelektriti kondenzator kapacitivnosti 100 μF; predupor ima upornost 1 kΩ. Ovrednotimo prehodni pojav. ⇒ Časovna konstanta τ = RC je 100 ms. Praktični čas prehodnega pojava je 0,5 s. Začetna vrednost toka je U / R = 0,5 A, v nadaljevanju pa je
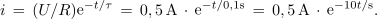
V času časovne konstante je vrednost toka 185 mA, po petih časovnih konstantah pa le še 3,5 mA. Napetost na kondenzatorju določa funkcija
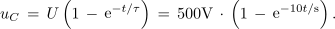
V času ene časovne konstante je napetost na njem 335 V, po petih pa že 496 V.
Opombe
- ↑ Tangenta na krivuljo v kateremkoli trenutku t1 seka abscisno os v točki t1 + τ.
Podpoglavja:
- 5.8.1 Polnjenje kondenzatorja z začetno prednapetostjo
- 5.8.2 Polnjenje kondenzatorja s tokovnim virom
| | 5.8.1 Polnjenje kondenzatorja z začetno prednapetostjo |