Iz e-ELEKTROTEHNIKA plus
Prvotno vezje dogradimo s še enim uporom in s tripolnim stikalom (slika 5). Ko je pretikalo v položaju 1, se kondenzator polni s tokom skozi upor upornosti R1, ko pa je v položaju 2, se kondenzator prazni s tokom skozi oba upora. Takole: ob času t0, ko pretikalo pretaknemo v prvi položaj, naj je kondentator prazen. Zatem se začne polniti in ob času t1 doseže npr. napetost U1; nakar pretikalo pretaknemo v drugo lego. Vzpostavi se vezje, v katerem ni vira, pridružuje pa se upor upornosti R2. Za katerikoli čas t > t1 zapišimo zančno in povezujoče enačbe:
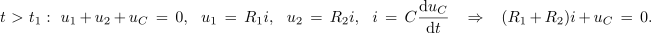
Napetostno enačbo odvedemo in vanjo uvedemo enačbo kondenzatorja:
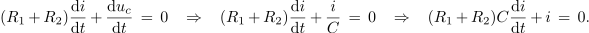
Za produkt vsote upornosti in kapacitivnosti vpeljemo konstanto τ12, kar dá:
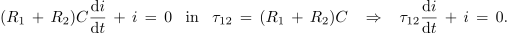
Enačba je podobna prejšnji za polnilni tok; zadošča ji funkcija:
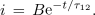
Ker je napetost na kondenzatorju tik po preklopu še vedno enaka U1, je:
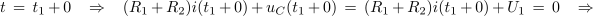
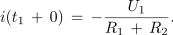
Predznak kaže na to, da je smer praznilnega nasprotna smeri polnilnega toka. Ko to vrednost upoštevamo v funkciji praznilnega toka, dobimo konstanto B,
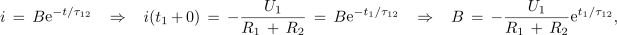
in tudi rešitev za ta tok:
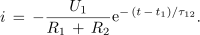
Dinamiko določa konstanta τ12; za sosledje je odgovoren čas t - t1, ki ustreza času, štetemu od zadnjega preklopa (slika 6). Napetosti na kondenzatorju in uporih so:
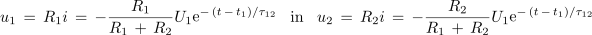
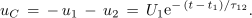
Vso toploto, ki se sprosti v uporih od t1 do kasnejšega časa t2, določa integral:
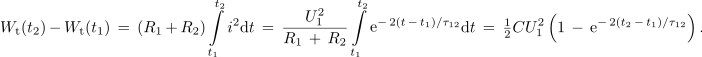
Ko je čas t2 - t1 nekajkratnik časovne konstante, je množina toplote v uporih enaka ravno tisti, ki se je do zadnjega preklopa akumulirala v kondenzatorju.
 5.8.2 Polnjenje kondenzatorja s tokovnim virom
| 5.10 Polnjenje tuljave
|
