Iz e-ELEKTROTEHNIKA plus
Iskanje nedoločenega integrala funkcije f ustreza poizvedovanju po tisti funkciji F, katere odvod je funkcija f:
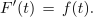
Odvajanje in integriranje sta si inverzni operaciji; kot sta si inverzni naprimer potenciranje in korenjenje. Ko enkrat znamo katerokoli število (x) kvadrirati, se lotimo korenjenja: da iščemo tisto število X, katerega kvadrat je x; in nekaj podobnega je tudi z odvajanjem in integriranjem. Ko imamo na zalogi dovolj bogate izkušnje z odvodi, se lotimo tudi nedoločenih integralov funkcij[1].
Potenčna funkcija.
Odvoda konstantne in linearne funkcije smo že osvetlili; naslednja bodi morda kar funkcija f(t) = t3; njen odvod najdemo po definiciji:
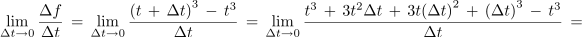
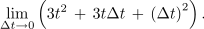
Ko Δt stremi k nič, se zadnja dva sumanda manjšata in postajata neznatna do prvega, zato je:
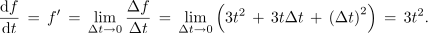
Odvod funkcije t3 je funkcija 3t2; na podoben način bi izvedli odvod potenčne funkcije n-te stopnje; dobili bi:
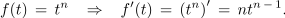
Pravilo je: eksponent potenčne funkcije se zmanjša za ena, prvotni pa se kot multiplikator seli pred novo potenčno funkcijo. Povsem enako pravilo velja tudi pri funkcijah necelih eksponentov.
Sedaj pa še nedoločen integral oziroma F(t) funkcije f(t) = t3. Funkcija F(t) je enaka vsoti četrtine potenčne funkcije četrte stopnje in poljubne konstante:
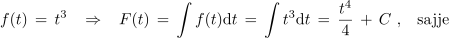
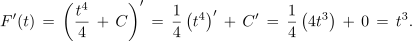
Splošno pravilo je:
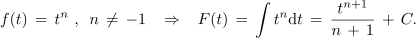
Zgled 1. V nekem časovnem intervalu določa tok skozi tuljavo induktivnosti L izraz i = at2 - bt + c. Izrazimo napetost na tuljavi! ⇒ Izhajamo iz enačbe tuljave:
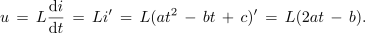
Zgled 2. Med časoma t1 in t2 podaja tok skozi upor upornosti R izraz i = at - b. Izrazimo množino toplote med tema časoma! ⇒ Sproščeno toploto določa integral moči p = Ri2:
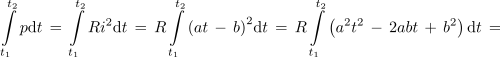
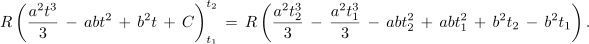
Harmonična funkcija.
Z njeno strmino, ki preide v limiti v odvod, smo se že spopadli. Takrat smo to opravili na geometrijski način, tokrat pa takole[2]:
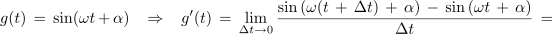
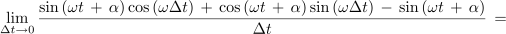
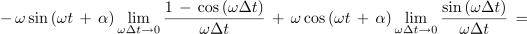
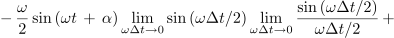
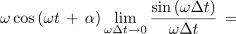
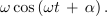
Če bi podobno postopali tudi pri kosinusni funkciji, bi dobili:
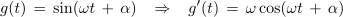
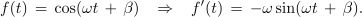
Iz odvodov razberemo pravili: odvod sinusne je kosinusna funkcija in odvod kosinusne je negativna sinusna funkcija. Pri odvodih se konstanta ω prenese iz argumenta v multiplikator s funkcijo. Za harmonični funkciji moremo brž najti še nedoločena integrala:
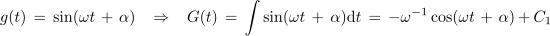
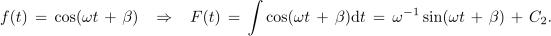
Zgled 3. Pri analizi harmonično vzbujanih reaktivnih elementov smo ugotovili, da je moč dotekanja energije v njih harmonična časovna funkcija, katere amplituda ustreza jalovi moči Q. Trenutno moč p(t) naj določa izraz Qsin(2ωt), v katerem je ω krožna frekvenca toka oziroma napetosti. V prvi četrtini periode toka (napetosti) je moč pozitivna in element se polni, drugo četrtino periode se element prazni itn. V trenutku t0 = 0 s naj je element brez energije, W(t0) = 0 J. Določimo energijo v elementu v kasnejšem času t1! ⇒ Moč je odvod energije, zato veljajo zveze:
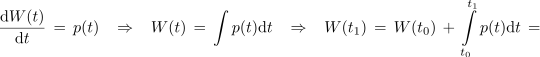
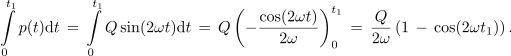
Največja energija je v elementu takrat, ko ima kosinusna funkcija vrednost -1; enaka je Q / ω. Poprečna energija je polovica tega, torej Q / 2ω. Če ima tuljava jalovo moč 2 kvar, bo pri 50 Hz poprečna energija v njej 3,18 J, največja pa 6,36 J. Slednja je sicer majhna, vendar se moramo zavedati, da je v eni sekundi pride ali odide sto-krat toliko.
Eksponentna funkcija.
Zapisali jo bomo v obliki
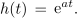
Matematična funkcija terja v argumentu neimenovano število; pri času t ima konstanta a enoto s-1; nekaj podobnega smo zasledili pri argumentu (kotu ωt) harmonične funkcije. Poiščimo odvod eksponentne funkcije[3]:
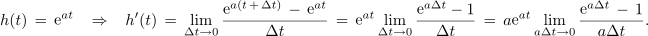
Limitiranje uženemo z vpeljavo spremenljivke s,
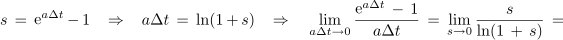
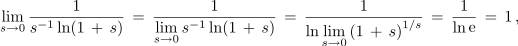
kar končno da:
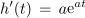
Posebnost eksponentne funkcije je v tem, da se odvod in integral izražata z njo samo:
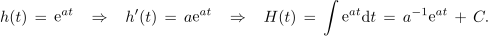
Zgled 4. Polnilni tok kondenzatorja, ki je ob t0 = 0 prazen, je i = 10 mA.e-t / 2 s; Q(t0) = 0 C. Ob t0 = 0 je jakost toka 10 mA, po dveh sekundah 10 mA / e, po štirih 10 mA / e2, po šestih 10 mA / e3, po 10 s pa komaj še 10 mA / e5 ≅ 0,067 mA, kar ustreza komaj 2/3 % začetnega toka. Izračunajmo naboj, ki priteče na ploščo do 10 sekunde! ⇒ Račun je podoben prejšnjemu. Tok je odvod naboja:
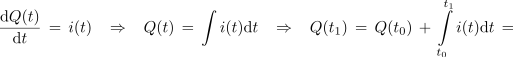
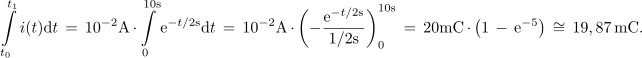
Po zelo (zelo) dolgem času bo naboj dosegel vrednost 20 mC.
Opombe
- ↑ Pri praktični uporabi infinitezimalnega računa se pokaže, da je funkcij, katerim moremo najti tiste, katerih odvodi so, neprimerno manj, kot tistih, katerim takšnih nikakor ne uspemo najti. V tem primeru določen in nedoločen integral nista povezana, saj nedoločenega kratkomalo ni. Ker pa je naša naloga, ovrednotiti predvsem določen integral, nedoločen je temu le v pomoč, ostaja na voljo vrsta numeričnih poti oziroma približkov določenega integrala, ki se opirajo na vsoti Sn, Zn ali katerokoli drugo, ki je njima blizu.
- ↑ Iz matematike vemo, da je
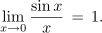
- ↑ Iz matematike vemo, da je
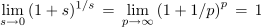
Podpoglavja:
| | 5.7.1 Potenčna funkcija |
