Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| Vrstica 1: | Vrstica 1: | ||
| + | [[Image:eele_slika_3_4_2.svg|thumb|right|Slika 3.4.2]] | ||
| + | [[Image:eele_slika_3_4_3.svg|thumb|right|Slika 3.4.3]] | ||
| + | |||
<primer> | <primer> | ||
'''Primer:''' | '''Primer:''' | ||
Redakcija: 07:37, 3. maj 2010
![](javascript: loadPicture("Eele_slika_3_4_2.svg", 551);)
![](javascript: loadPicture("Eele_slika_3_4_3.svg", 836);)
Primer:
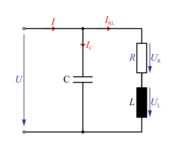
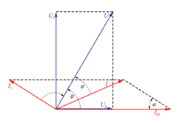
Primer: Izračunaj toke, impedanco in fazni kot φ v izmeničnem krogu, ki ga prikazuje slika 3.4.2. Napetost izvora U = 230 V / 50 Hz, R = 20 Ω, L = 1 H in C = 4 μF.Slika 3.4.2V izmeničnih krogih s sestavljenimi vezavami upornosti nimamo skupne količine vseh elementov, zato pri risanju kazalčnih diagramov izberemo najprej za izhodiščno količino skupno količino določenega dela vezave. V našem primeru je to tok IRL (sl. 3.4.2 in 3.4.3). Napetost na ohmski upornosti je s tokom IRL v fazi napetost na induktivni upornosti pa prehiteva tok IRL za 90 º. Geometrična vsota napetosti na ohmski in induktivni upornosti je enaka napetosti izvora U, kapacitivni tok IC pa prehiteva napetost izvora za 90 º. Tok izvora je enak geometrični vsoti tokov IR in IC. Slika 3.4.3Impedanca veje z uporom in tuljavo:
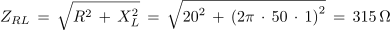
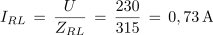
Upornost in tok kapacitivne veje:
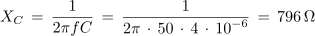
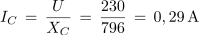
Ker kazalca tokov IRL in IC nista med seboj pravokotna, ne tvorita s svojo geometrično vsoto pravokotnega trikotnika. V trikotniku, ki ni pravokotnem, pa si moramo namesto s Pitagorovim pomagati s kosinusovim izrekom, kar za hitrejše računanje ni najbolj simpatično:
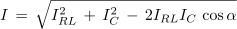
Za določitev kota α potrebujemo kot φ1:
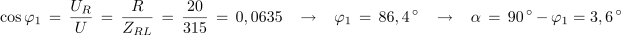
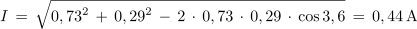
Impedanca vezave:
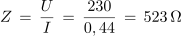
In končno še fazni kot med napetostjo in tokom izvora:
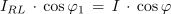
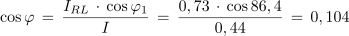
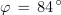
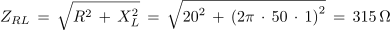
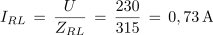
Upornost in tok kapacitivne veje:
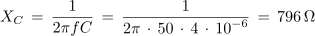
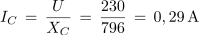
Ker kazalca tokov IRL in IC nista med seboj pravokotna, ne tvorita s svojo geometrično vsoto pravokotnega trikotnika. V trikotniku, ki ni pravokotnem, pa si moramo namesto s Pitagorovim pomagati s kosinusovim izrekom, kar za hitrejše računanje ni najbolj simpatično:
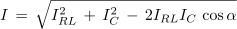
Za določitev kota α potrebujemo kot φ1:
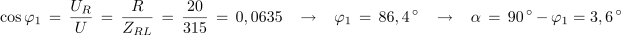
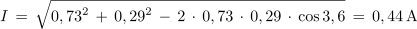
Impedanca vezave:
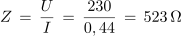
In končno še fazni kot med napetostjo in tokom izvora:
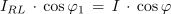
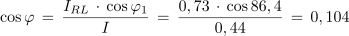
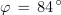
Na osnovi kazalčnega diagrama (slika 3.4.3) in računa lahko ugotovimo:
- Količine izmeničnih krogov s sestavljenimi vezavami uporov, tuljav in kondenzatorjev tvorijo tudi nepravokotne trikotnike.
Računanje v nepravokotnih trikotnikih je, še posebej pri zahtevnejših sestavljenih vezavah, nepregledno, dolgotrajno in naporno. Obstaja sicer še način, pri katerem najprej pretvorimo sestavljeno vezavo v enakovredno čisto zaporedno ali vzporedno vezavo, toda na ta način izgubimo fizikalno sliko vezave, ki je v čistih vezavah bila dokaj jasna in je prispevala k razumljivosti poteka računa in samega rezultata.
Zato se, še posebej v zahtevnejših primerih, obema načinoma izogibamo in na pomoč pokličemo elegantnejšo in preglednejšo pot računanja v kompleksni ravnini.
 4.1 Računanje v zahtevnejših izmeničnih krogih
| 4.1.2 Računanje električnih količin v kompleksi ravnini
|
