Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| (2 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
| - | Spremenjeno polnilno vezje vzbuja realen tokovni vir (slika | + | [[Slika:eele_slika_visji_101.svg|thumb|Slika 101: Polnitev kondenzatorja s tokovnim virom; vrednost končne napetosti kondenzatorja določa vzporeden upor upornosti <latex>R</latex>.]] |
| + | |||
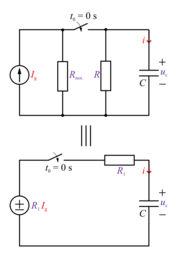
| + | Spremenjeno polnilno vezje vzbuja realen tokovni vir (slika 101). Pred vklopom stikala ob ''t''<sub>0</sub> = 0 s naj bo kondenzator prazen. Nadaljujemo takole. Zunanji in notranji upor združimo v nadomestnega z upornostjo | ||
| + | |||
<latex>{R_1}\, =\, R{R_{{\rm{not}}{\rm{.}}}}/(R \,+\, {R_{{\rm{not}}{\rm{.}}}}).</latex> | <latex>{R_1}\, =\, R{R_{{\rm{not}}{\rm{.}}}}/(R \,+\, {R_{{\rm{not}}{\rm{.}}}}).</latex> | ||
| - | Tokovnemu viru s tokom ''I''<sub>g</sub> in vzporednemu uporu z upornostjo ''R''<sub>1</sub> priredimo realen napetostni vir | + | |
| + | Tokovnemu viru s tokom ''I''<sub>g</sub> in vzporednemu uporu z upornostjo ''R''<sub>1</sub> priredimo realen napetostni vir, tvorita ga idealni vir z napetostjo ''R''<sub>1</sub>''I''<sub>g</sub> in zaporedni upor z upornostjo ''R''<sub>1</sub>, torej vezje, ki je (skupaj s kondenzatorjem) enako prvotnemu polnilnemu vezju. Če je pa tako, smemo od tam prepisati tudi rešitev: | ||
| + | |||
<latex>{u_C} \,= \,{R_1}{I_{\rm{g}}}\left( {1 \,-\, {{\mathop{\rm e}\nolimits} ^{ - t/\tau }}} \right)\, = \,\frac{R{R_{{\rm{not}}{\rm{.}}}}}{R + {R_{{\rm{not}}{\rm{.}}}}}{I_{\rm{g}}}\left( {1\, -\, {{\mathop{\rm e}\nolimits} ^{ - t/\tau }}} \right){\rm{ \,\,\,\,\,in \,\,\,\,\, }}\tau \, =\, {R_1}C.</latex> | <latex>{u_C} \,= \,{R_1}{I_{\rm{g}}}\left( {1 \,-\, {{\mathop{\rm e}\nolimits} ^{ - t/\tau }}} \right)\, = \,\frac{R{R_{{\rm{not}}{\rm{.}}}}}{R + {R_{{\rm{not}}{\rm{.}}}}}{I_{\rm{g}}}\left( {1\, -\, {{\mathop{\rm e}\nolimits} ^{ - t/\tau }}} \right){\rm{ \,\,\,\,\,in \,\,\,\,\, }}\tau \, =\, {R_1}C.</latex> | ||
| - | Iz nje prepoznavamo vlogo upornosti ''R'' oziroma upora, ki je v izhodiščnem vezju vzporeden h kondenzatorju (da določa končno napetost kondenzatorja, h kateri se eksponentno približuje), | + | |
| + | Iz nje prepoznavamo vlogo upornosti ''R'' oziroma upora, ki je v izhodiščnem vezju vzporeden h kondenzatorju (da določa končno napetost kondenzatorja, h kateri se eksponentno približuje), pridobimo pa lahko tudi rešitve za druge količine v prvotnem polnilnem vezju, in sicer: | ||
| + | |||
<latex>{u_R}\, =\, {u_C},\,\,\,{\rm{ }}{i_C}\, = \,C\frac{{\rm{d}}{u_C}}{{\rm{d}}t}\, =\, C{R_1}{I_{\rm{g}}}\frac{1}{\tau }{{\mathop{\rm e}\nolimits} ^{ - t/\tau }} \,=\, {I_{\rm{g}}}{{\mathop{\rm e}\nolimits} ^{ - t/\tau }}{\rm{,\,\,\,\, }}{i_R}\, =\, \frac{u_R}{R}\, =\,\frac{R_{{\rm{not}}{\rm{.}}}}{R\, +\, {R_{{\rm{not}}{\rm{.}}}}}{I_{\rm{g}}}\left( {1\, -\, {{\mathop{\rm e}\nolimits} ^{ - t/\tau }}} \right),</latex> | <latex>{u_R}\, =\, {u_C},\,\,\,{\rm{ }}{i_C}\, = \,C\frac{{\rm{d}}{u_C}}{{\rm{d}}t}\, =\, C{R_1}{I_{\rm{g}}}\frac{1}{\tau }{{\mathop{\rm e}\nolimits} ^{ - t/\tau }} \,=\, {I_{\rm{g}}}{{\mathop{\rm e}\nolimits} ^{ - t/\tau }}{\rm{,\,\,\,\, }}{i_R}\, =\, \frac{u_R}{R}\, =\,\frac{R_{{\rm{not}}{\rm{.}}}}{R\, +\, {R_{{\rm{not}}{\rm{.}}}}}{I_{\rm{g}}}\left( {1\, -\, {{\mathop{\rm e}\nolimits} ^{ - t/\tau }}} \right),</latex> | ||
| + | |||
<latex>i\, =\, {i_C} \,+ \,{i_R} \,=\, {I_{\rm{g}}}{{\mathop{\rm e}\nolimits} ^{ - t/\tau }}\, + \,\frac{{{R_{{\rm{not}}{\rm{.}}}}}}{{R \,+ \,{R_{{\rm{not}}{\rm{.}}}}}}{I_{\rm{g}}}\left( {1 \,- \,{{\mathop{\rm e}\nolimits} ^{ - t/\tau }}} \right)\, =\, \frac{{{R_{{\rm{not}}{\rm{.}}}}}}{{R\, +\, {R_{{\rm{not}}{\rm{.}}}}}}{I_{\rm{g}}}\, + \,\frac{R}{{R \,+ \,{R_{{\rm{not}}{\rm{.}}}}}}{I_{\rm{g}}}{{\mathop{\rm e}\nolimits} ^{ - t/\tau }}.</latex> | <latex>i\, =\, {i_C} \,+ \,{i_R} \,=\, {I_{\rm{g}}}{{\mathop{\rm e}\nolimits} ^{ - t/\tau }}\, + \,\frac{{{R_{{\rm{not}}{\rm{.}}}}}}{{R \,+ \,{R_{{\rm{not}}{\rm{.}}}}}}{I_{\rm{g}}}\left( {1 \,- \,{{\mathop{\rm e}\nolimits} ^{ - t/\tau }}} \right)\, =\, \frac{{{R_{{\rm{not}}{\rm{.}}}}}}{{R\, +\, {R_{{\rm{not}}{\rm{.}}}}}}{I_{\rm{g}}}\, + \,\frac{R}{{R \,+ \,{R_{{\rm{not}}{\rm{.}}}}}}{I_{\rm{g}}}{{\mathop{\rm e}\nolimits} ^{ - t/\tau }}.</latex> | ||
| + | |||
Tik po vklopu je tok skozi stikalo enak ''I''<sub>g</sub>, po nekaj časovnih konstantah pa se ustali na vrednosti, ki jo določa delilnik uporov upornosti ''R'' in ''R''<sub>not</sub>. Brž, ko bi stikalo ob nekem poznejšem času izklopili, bi se kondenzator izpraznil skozi njemu vzporeden upor. | Tik po vklopu je tok skozi stikalo enak ''I''<sub>g</sub>, po nekaj časovnih konstantah pa se ustali na vrednosti, ki jo določa delilnik uporov upornosti ''R'' in ''R''<sub>not</sub>. Brž, ko bi stikalo ob nekem poznejšem času izklopili, bi se kondenzator izpraznil skozi njemu vzporeden upor. | ||
{{Hierarchy footer}} | {{Hierarchy footer}} | ||
Trenutna redakcija s časom 14:06, 15. avgust 2010
![](javascript: loadPicture("Eele_slika_visji_101.svg", 550);)
Spremenjeno polnilno vezje vzbuja realen tokovni vir (slika 101). Pred vklopom stikala ob t0 = 0 s naj bo kondenzator prazen. Nadaljujemo takole. Zunanji in notranji upor združimo v nadomestnega z upornostjo
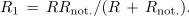
Tokovnemu viru s tokom Ig in vzporednemu uporu z upornostjo R1 priredimo realen napetostni vir, tvorita ga idealni vir z napetostjo R1Ig in zaporedni upor z upornostjo R1, torej vezje, ki je (skupaj s kondenzatorjem) enako prvotnemu polnilnemu vezju. Če je pa tako, smemo od tam prepisati tudi rešitev:
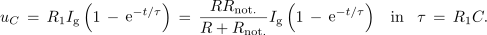
Iz nje prepoznavamo vlogo upornosti R oziroma upora, ki je v izhodiščnem vezju vzporeden h kondenzatorju (da določa končno napetost kondenzatorja, h kateri se eksponentno približuje), pridobimo pa lahko tudi rešitve za druge količine v prvotnem polnilnem vezju, in sicer:
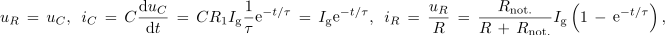
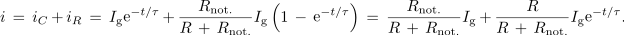
Tik po vklopu je tok skozi stikalo enak Ig, po nekaj časovnih konstantah pa se ustali na vrednosti, ki jo določa delilnik uporov upornosti R in Rnot. Brž, ko bi stikalo ob nekem poznejšem času izklopili, bi se kondenzator izpraznil skozi njemu vzporeden upor.
 5.8.1 Polnjenje kondenzatorja z začetno prednapetostjo
| 5.9 Praznjenje kondenzatorja
|
