Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| (3 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
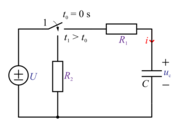
| - | Prvotno vezje dogradimo s še enim uporom in s tripolnim stikalom (slika | + | [[Slika:eele_slika_visji_099.svg|thumb|Slika 99: V zgornjem položaju pretikala se kondenzator polni, v spodnjem pa prazni.]] |
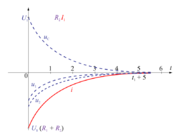
| + | [[Slika:eele_slika_visji_100.svg|thumb|Slika 100: Časovni diagrami toka in napetosti na elementih v času praznjenja kondenzatorja.]] | ||
| + | Prvotno vezje dogradimo s še enim uporom in s tripolnim stikalom (slika 99). Ko je pretikalo v položaju 1, se kondenzator polni s tokom skozi upor upornosti ''R''<sub>1</sub>, ko pa je v položaju 2, se kondenzator prazni s tokom skozi oba upora. Takole: ob času ''t''<sub>0</sub>, ko pretikalo pretaknemo v prvi položaj, naj bo kondentator prazen. Zatem se začne polniti in ob času ''t''<sub>1</sub> doseže npr. napetost ''U''<sub>1</sub>, nakar pretikalo pretaknemo v drugo lego. Vzpostavi se vezje, v katerem ni vira, pridružuje pa se upor upornosti ''R''<sub>2</sub>. Za katerikoli čas ''t'' > ''t''<sub>1</sub> zapišimo zančno in povezujoče enačbe: | ||
| + | |||
<latex>t\,\, \textgreater \,\,{t_1}:\,\,{\rm{ }}{u_1}\, +\, {u_2} \,+\, {u_C}\, = \,0,\,\,\,\,{\rm{ }}{u_1}\, = \,{R_1}i,\,\,\,\,{\rm{ }}{u_2}\, =\, {R_2}i,\,\,\,\,{\rm{ }}i\, =\, C\frac{{\rm{d}}{u_C}}{{\rm{d}}t}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ (}}{R_1}\, +\, {R_2})i\, + \,{u_C}\, =\, 0.</latex> | <latex>t\,\, \textgreater \,\,{t_1}:\,\,{\rm{ }}{u_1}\, +\, {u_2} \,+\, {u_C}\, = \,0,\,\,\,\,{\rm{ }}{u_1}\, = \,{R_1}i,\,\,\,\,{\rm{ }}{u_2}\, =\, {R_2}i,\,\,\,\,{\rm{ }}i\, =\, C\frac{{\rm{d}}{u_C}}{{\rm{d}}t}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ (}}{R_1}\, +\, {R_2})i\, + \,{u_C}\, =\, 0.</latex> | ||
| + | |||
Napetostno enačbo odvedemo in vanjo uvedemo enačbo kondenzatorja: | Napetostno enačbo odvedemo in vanjo uvedemo enačbo kondenzatorja: | ||
| + | |||
<latex>{\rm{(}}{R_1}\, +\, {R_2})\frac{{\rm{d}}i}{{\rm{d}}t}\, +\, \frac{{\rm{d}}{u_c}}{{\rm{d}}t}\, =\, 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ (}}{R_1} \,+\, {R_2})\frac{{\rm{d}}i}{{\rm{d}}t}\, +\, \frac{i}{C} \,=\, 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ (}}{R_1}\, +\, {R_2})C\frac{{\rm{d}}i}{{\rm{d}}t}\, +\, i\, =\, 0.</latex> | <latex>{\rm{(}}{R_1}\, +\, {R_2})\frac{{\rm{d}}i}{{\rm{d}}t}\, +\, \frac{{\rm{d}}{u_c}}{{\rm{d}}t}\, =\, 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ (}}{R_1} \,+\, {R_2})\frac{{\rm{d}}i}{{\rm{d}}t}\, +\, \frac{i}{C} \,=\, 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ (}}{R_1}\, +\, {R_2})C\frac{{\rm{d}}i}{{\rm{d}}t}\, +\, i\, =\, 0.</latex> | ||
| + | |||
Za produkt vsote upornosti in kapacitivnosti vpeljemo konstanto ''τ''<sub>12</sub>, kar dá: | Za produkt vsote upornosti in kapacitivnosti vpeljemo konstanto ''τ''<sub>12</sub>, kar dá: | ||
| + | |||
<latex>{\rm{(}}{R_1}\, +\, {R_2})C\frac{{\rm{d}}i}{{\rm{d}}t}\, +\, i\, = \,0\,\,\,\,\,{\rm{ in }}\,\,\,\,\,{\tau _{12}}\, = \,{\rm{(}}{R_1}\, +\,{R_2})C{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{\tau _{12}}\frac{{\rm{d}}i}{{\rm{d}}t}\, +\, i\, =\, 0.</latex> | <latex>{\rm{(}}{R_1}\, +\, {R_2})C\frac{{\rm{d}}i}{{\rm{d}}t}\, +\, i\, = \,0\,\,\,\,\,{\rm{ in }}\,\,\,\,\,{\tau _{12}}\, = \,{\rm{(}}{R_1}\, +\,{R_2})C{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{\tau _{12}}\frac{{\rm{d}}i}{{\rm{d}}t}\, +\, i\, =\, 0.</latex> | ||
| - | Enačba je podobna prejšnji za polnilni tok | + | |
| + | Enačba je podobna prejšnji za polnilni tok, zadošča ji funkcija: | ||
| + | |||
<latex>i\, =\, B{{\mathop{\rm e}\nolimits} ^{ - t/{\tau _{12}}}}.</latex> | <latex>i\, =\, B{{\mathop{\rm e}\nolimits} ^{ - t/{\tau _{12}}}}.</latex> | ||
| + | |||
Ker je napetost na kondenzatorju tik po preklopu še vedno enaka ''U''<sub>1</sub>, je: | Ker je napetost na kondenzatorju tik po preklopu še vedno enaka ''U''<sub>1</sub>, je: | ||
| + | |||
<latex>t \,= \,{t_1} \,+\, 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ (}}{R_1} \,+\, {R_2})i({t_1} \,+\, 0)\, +\, {u_C}({t_1}\, +\, 0) \,=\,{\rm{(}}{R_1}\, +\, {R_2})i({t_1}\, +\, 0) \,+\, {U_1} \,=\, 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}</latex> | <latex>t \,= \,{t_1} \,+\, 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ (}}{R_1} \,+\, {R_2})i({t_1} \,+\, 0)\, +\, {u_C}({t_1}\, +\, 0) \,=\,{\rm{(}}{R_1}\, +\, {R_2})i({t_1}\, +\, 0) \,+\, {U_1} \,=\, 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}</latex> | ||
| + | |||
<latex>i({t_1} \,+\, 0)\, =\, - \frac{U_1}{{R_1} \,+\, {R_2}}.</latex> | <latex>i({t_1} \,+\, 0)\, =\, - \frac{U_1}{{R_1} \,+\, {R_2}}.</latex> | ||
| + | |||
Predznak kaže na to, da je smer praznilnega nasprotna smeri polnilnega toka. Ko to vrednost upoštevamo v funkciji praznilnega toka, dobimo konstanto ''B'', | Predznak kaže na to, da je smer praznilnega nasprotna smeri polnilnega toka. Ko to vrednost upoštevamo v funkciji praznilnega toka, dobimo konstanto ''B'', | ||
| + | |||
<latex>i\, =\, B{{\mathop{\rm e}\nolimits} ^{ - t/{\tau _{12}}}}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}i({t_1}\, +\, 0)\, =\,- \frac{U_1}{{R_1} \,+\, {R_2}}\, =\, B{{\mathop{\rm e}\nolimits} ^{ - {t_1}/{\tau _{12}}}}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}B \,=\, - \frac{U_1}{{R_1} \,+\, {R_2}}{{\mathop{\rm e}\nolimits} ^{{t_1}/{\tau _{12}}}},</latex> | <latex>i\, =\, B{{\mathop{\rm e}\nolimits} ^{ - t/{\tau _{12}}}}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}i({t_1}\, +\, 0)\, =\,- \frac{U_1}{{R_1} \,+\, {R_2}}\, =\, B{{\mathop{\rm e}\nolimits} ^{ - {t_1}/{\tau _{12}}}}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}B \,=\, - \frac{U_1}{{R_1} \,+\, {R_2}}{{\mathop{\rm e}\nolimits} ^{{t_1}/{\tau _{12}}}},</latex> | ||
| + | |||
in tudi rešitev za ta tok: | in tudi rešitev za ta tok: | ||
| + | |||
<latex>{i\, =\, - \frac{U_1}{{R_1}\, +\, {R_2}}{{\mathop{\rm e}\nolimits} ^{ -\, (t\, -\, {t_1})/{\tau _{12}}}}.}</latex> | <latex>{i\, =\, - \frac{U_1}{{R_1}\, +\, {R_2}}{{\mathop{\rm e}\nolimits} ^{ -\, (t\, -\, {t_1})/{\tau _{12}}}}.}</latex> | ||
| - | Dinamiko določa konstanta ''τ''<sub>12</sub> | + | |
| + | Dinamiko določa konstanta ''τ''<sub>12</sub>, za sosledje je odgovoren čas ''t'' - ''t''<sub>1</sub>, ki ustreza času, štetemu od zadnjega preklopa (slika 100). Napetosti na kondenzatorju in uporih so: | ||
| + | |||
<latex>{u_1} \,=\, {R_1}i \,=\, - \frac{R_1}{{R_1}\, +\, {R_2}}{U_1}{{\mathop{\rm e}\nolimits} ^{ - \,(t \,-\, {t_1})/{\tau _{12}}}}{\rm{ \,\,\,\,\, in \,\,\,\,\, }}{u_2} \,=\, {R_2}i \,=\, - \frac{R_2}{{R_1}\, + \,{R_2}}{U_1}{{\mathop{\rm e}\nolimits} ^{ - \,(t\, -\,{t_1})/{\tau _{12}}}}</latex> | <latex>{u_1} \,=\, {R_1}i \,=\, - \frac{R_1}{{R_1}\, +\, {R_2}}{U_1}{{\mathop{\rm e}\nolimits} ^{ - \,(t \,-\, {t_1})/{\tau _{12}}}}{\rm{ \,\,\,\,\, in \,\,\,\,\, }}{u_2} \,=\, {R_2}i \,=\, - \frac{R_2}{{R_1}\, + \,{R_2}}{U_1}{{\mathop{\rm e}\nolimits} ^{ - \,(t\, -\,{t_1})/{\tau _{12}}}}</latex> | ||
| + | |||
<latex>{u_C}\, =\, - \,{u_1}\, -\, {u_2} \,=\, {U_1}{{\mathop{\rm e}\nolimits} ^{ -\, (t\, -\, {t_1})/{\tau _{12}}}}.</latex> | <latex>{u_C}\, =\, - \,{u_1}\, -\, {u_2} \,=\, {U_1}{{\mathop{\rm e}\nolimits} ^{ -\, (t\, -\, {t_1})/{\tau _{12}}}}.</latex> | ||
| + | |||
Vso toploto, ki se sprosti v uporih od ''t''<sub>1</sub> do kasnejšega časa ''t''<sub>2</sub>, določa integral: | Vso toploto, ki se sprosti v uporih od ''t''<sub>1</sub> do kasnejšega časa ''t''<sub>2</sub>, določa integral: | ||
| + | |||
<latex>{W_{\rm{t}}}({t_2}) \,-\, {W_{\rm{t}}}({t_1}) \,=\, ({R_1} \,+\, {R_2})\int\limits_{t_1}^{t_2} {{i^{\rm{2}}}{\rm{d}}t} \, =\,\frac{U_1^2}{{R_1}\, +\, {R_2}}\int\limits_{t_1}^{t_2} {{{\mathop{\rm e}\nolimits} ^{ -\, 2(t \,-\, {t_1})/{\tau _{12}}}}{\rm{d}}t}\, =\, {\textstyle{1 \over 2}}CU_1^2\left( {1\, -\, {{\rm{e}}^{ - \,2({t_2} \,-\, {t_1}{\rm{)/}}{\tau _{12}}}}} \right).</latex> | <latex>{W_{\rm{t}}}({t_2}) \,-\, {W_{\rm{t}}}({t_1}) \,=\, ({R_1} \,+\, {R_2})\int\limits_{t_1}^{t_2} {{i^{\rm{2}}}{\rm{d}}t} \, =\,\frac{U_1^2}{{R_1}\, +\, {R_2}}\int\limits_{t_1}^{t_2} {{{\mathop{\rm e}\nolimits} ^{ -\, 2(t \,-\, {t_1})/{\tau _{12}}}}{\rm{d}}t}\, =\, {\textstyle{1 \over 2}}CU_1^2\left( {1\, -\, {{\rm{e}}^{ - \,2({t_2} \,-\, {t_1}{\rm{)/}}{\tau _{12}}}}} \right).</latex> | ||
| + | |||
Ko je čas ''t''<sub>2</sub> - ''t''<sub>1</sub> nekajkratnik časovne konstante, je množina toplote v uporih enaka ravno tisti, ki se je do zadnjega preklopa akumulirala v kondenzatorju. | Ko je čas ''t''<sub>2</sub> - ''t''<sub>1</sub> nekajkratnik časovne konstante, je množina toplote v uporih enaka ravno tisti, ki se je do zadnjega preklopa akumulirala v kondenzatorju. | ||
{{Hierarchy footer}} | {{Hierarchy footer}} | ||
Trenutna redakcija s časom 14:10, 15. avgust 2010
![](javascript: loadPicture("Eele_slika_visji_099.svg", 534);)
![](javascript: loadPicture("Eele_slika_visji_100.svg", 800);)
Prvotno vezje dogradimo s še enim uporom in s tripolnim stikalom (slika 99). Ko je pretikalo v položaju 1, se kondenzator polni s tokom skozi upor upornosti R1, ko pa je v položaju 2, se kondenzator prazni s tokom skozi oba upora. Takole: ob času t0, ko pretikalo pretaknemo v prvi položaj, naj bo kondentator prazen. Zatem se začne polniti in ob času t1 doseže npr. napetost U1, nakar pretikalo pretaknemo v drugo lego. Vzpostavi se vezje, v katerem ni vira, pridružuje pa se upor upornosti R2. Za katerikoli čas t > t1 zapišimo zančno in povezujoče enačbe:
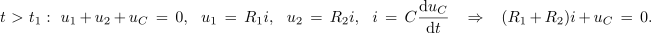
Napetostno enačbo odvedemo in vanjo uvedemo enačbo kondenzatorja:
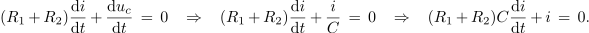
Za produkt vsote upornosti in kapacitivnosti vpeljemo konstanto τ12, kar dá:
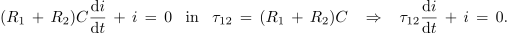
Enačba je podobna prejšnji za polnilni tok, zadošča ji funkcija:
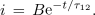
Ker je napetost na kondenzatorju tik po preklopu še vedno enaka U1, je:
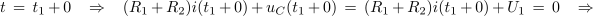
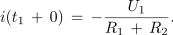
Predznak kaže na to, da je smer praznilnega nasprotna smeri polnilnega toka. Ko to vrednost upoštevamo v funkciji praznilnega toka, dobimo konstanto B,
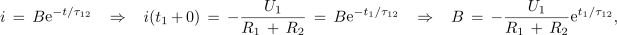
in tudi rešitev za ta tok:
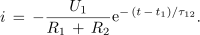
Dinamiko določa konstanta τ12, za sosledje je odgovoren čas t - t1, ki ustreza času, štetemu od zadnjega preklopa (slika 100). Napetosti na kondenzatorju in uporih so:
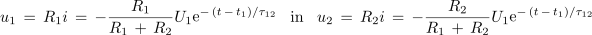
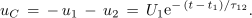
Vso toploto, ki se sprosti v uporih od t1 do kasnejšega časa t2, določa integral:
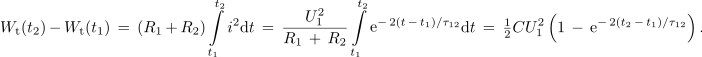
Ko je čas t2 - t1 nekajkratnik časovne konstante, je množina toplote v uporih enaka ravno tisti, ki se je do zadnjega preklopa akumulirala v kondenzatorju.
 5.8.2 Polnjenje kondenzatorja s tokovnim virom
| 5.10 Polnjenje tuljave
|
