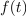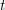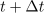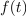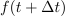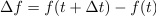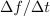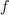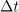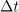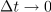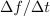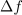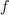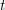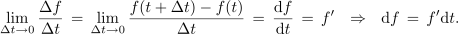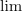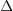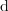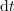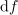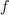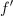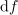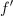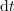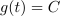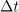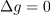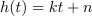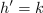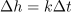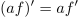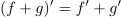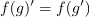Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
|
|
| Vrstica 1: |
Vrstica 1: |
| - | Imejmo časovno funkcijo <latex>f(t)</latex>, ki podaja napetost, morda moč, tok, naboj ali energijo (slika 1). Izberimo bližnja trenutka <latex>t</latex> in <latex>t+\Delta t</latex>. Upati smemo, da si bosta blizu tudi funkcijski vrednosti <latex>f(t)</latex> in <latex>f(t+\Delta t)</latex>. Prirastek <latex>\Delta f=f(t+\Delta t)-f(t)</latex> je pomemben, verjetno pa tudi kvocient <latex>\Delta f/\Delta t</latex>, ki ugotavlja hitrost spreminjanja funkcije <latex>f</latex>. Informacija o njej bo najboljša takrat, ko bo interval <latex>\Delta t</latex> kar najkrajši, ko bo <latex>\Delta t</latex> ''limitiral'' k nič, kar povzema zapis: <latex>\Delta t \to 0</latex>. Če bo tako, se bo nekaj limitnega dogajalo tudi s kvocientom <latex>\Delta f/\Delta t</latex>. Ko se bo manjšal imenovalec <latex>\Delta t</latex>, se bo z njim manjšal tudi števec <latex>\Delta f</latex>, in upamo lahko, da bo k neki vrednosti limitiral tudi njun kvocient. Vrednost, h kateri stremi, imenujemo ''odvod funkcije'' <latex>f</latex> ob času <latex>t</latex>. Odvod pišemo takole: | + | [[Slika:eele_slika_visji_092.svg|thumb|Slika 92: K opredelitvi odvoda časovne funkcije v trenutku <latex>t</latex>, ko prirastek <latex>\Delta t</latex> limitira k nič.]] |
| | + | Imejmo časovno funkcijo <latex>f(t)</latex>, ki podaja napetost, morda moč, tok, naboj ali energijo (slika 92). Izberimo bližnja trenutka <latex>t</latex> in <latex>t+\Delta t</latex>. Upati smemo, da si bosta blizu tudi funkcijski vrednosti <latex>f(t)</latex> in <latex>f(t+\Delta t)</latex>. Prirastek <latex>\Delta f=f(t+\Delta t)-f(t)</latex> je pomemben, verjetno pa tudi kvocient <latex>\Delta f/\Delta t</latex>, ki ugotavlja hitrost spreminjanja funkcije <latex>f</latex>. Informacija o njej bo najboljša takrat, ko bo interval <latex>\Delta t</latex> kar najkrajši, ko bo <latex>\Delta t</latex> ''limitiral'' k nič, kar povzema zapis: <latex>\Delta t \to 0</latex>. Če bo tako, se bo nekaj limitnega dogajalo tudi s kvocientom <latex>\Delta f/\Delta t</latex>. Ko se bo manjšal imenovalec <latex>\Delta t</latex>, se bo z njim manjšal tudi števec <latex>\Delta f</latex>, in upamo lahko, da bo k neki vrednosti limitiral tudi njun kvocient. Vrednost, h kateri stremi, imenujemo ''odvod funkcije'' <latex>f</latex> ob času <latex>t</latex>. Odvod pišemo takole: |
| | | | |
| | | | |
Trenutna redakcija s časom 13:15, 15. avgust 2010
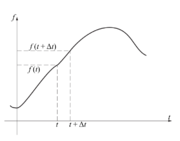
Slika 92: K opredelitvi odvoda časovne funkcije v trenutku
, ko prirastek
limitira k nič.
Imejmo časovno funkcijo
, ki podaja napetost, morda moč, tok, naboj ali energijo (slika 92). Izberimo bližnja trenutka
in
. Upati smemo, da si bosta blizu tudi funkcijski vrednosti
in
. Prirastek
je pomemben, verjetno pa tudi kvocient
, ki ugotavlja hitrost spreminjanja funkcije
. Informacija o njej bo najboljša takrat, ko bo interval
kar najkrajši, ko bo
limitiral k nič, kar povzema zapis:
. Če bo tako, se bo nekaj limitnega dogajalo tudi s kvocientom
. Ko se bo manjšal imenovalec
, se bo z njim manjšal tudi števec
, in upamo lahko, da bo k neki vrednosti limitiral tudi njun kvocient. Vrednost, h kateri stremi, imenujemo
odvod funkcije ob času
. Odvod pišemo takole:
Znak »
« je okrajšava za
limito, znak razlike »
« pa preide v
diferencialni znak »
«. Novi, infinitezimalni količini
in
sta
diferenciala neodvisne in odvisne spremenljivke. Ker je odvod funkcije
v splošnem tudi funkcija, se za odvod uporablja tudi nekvocientni zapis »
«. Diferencial
določa torej produkt odvoda
in diferenciala
.
Najpreprostejša je konstantna funkcija:
. Upodablja jo premica, ki je vzporedna abscisni osi. Pri vsakem intervalu
je
, odvod konstante je nič. Odvod linearne funkcije
je
, saj je
; o drugih več kasneje. Izpostavimo tudi nekaj lastnosti odvoda, te izhajajo iz definicije:
in
ter
.
Podpoglavja:
![](javascript: loadPicture("Eele_slika_visji_092.svg", 700);)
5.2 Kako analizirati prehodni pojav
