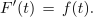|
|
| Vrstica 6: |
Vrstica 6: |
| | | | |
| | | | |
| - | == Potenčna funkcija ==
| + | <references /> |
| | | | |
| - | Odvoda konstantne in linearne funkcije smo že osvetlili. Naslednja naj bo morda kar funkcija ''f''(''t'') = ''t''<sup>3</sup>, njen odvod najdemo po definiciji:
| |
| - |
| |
| - | <latex>\mathop {\lim }\limits_{\Delta t \to 0} \frac{\Delta f}{\Delta t} \,= \,\mathop {\lim }\limits_{\Delta t \to 0} \frac{{{(t\, +\, \Delta t)}^3} \,- \,{t^3}}{\Delta t}\, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{{t^3}\, +\, 3{t^2}\Delta t \,+\, 3t{{(\Delta t)}^2}\, +\, {{(\Delta t)}^3} \,-\, {t^3}}{\Delta t}\, =\, </latex>
| |
| - |
| |
| - | <latex>\mathop {\lim }\limits_{\Delta t \to 0} \left( {3{t^2} \,+ \,3t\Delta t\, +\, {{(\Delta t)}^2}} \right).</latex>
| |
| - |
| |
| - | Ko Δ''t'' stremi k nič, se zadnja dva sumanda manjšata in postajata neznatna do prvega, zato je:
| |
| - |
| |
| - | <latex>\frac{{\rm{d}}f}{{\rm{d}}t} \,=\, f^\prime \, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{\Delta f}{\Delta t} \,= \,\mathop {\lim }\limits_{\Delta t \to 0} \left( {3{t^2}\, +\, 3t\Delta t \,+\, {{(\Delta t)}^2}} \right)\, =\, 3{t^2}.</latex>
| |
| - |
| |
| - | Odvod funkcije ''t''<sup>3</sup> je funkcija 3''t''<sup>2</sup>, na podoben način bi izvedli odvod potenčne funkcije ''n''-te stopnje. Dobili bi:
| |
| - |
| |
| - | <latex>{f(t) \,=\, {t^n}{\rm{ }}\,\,\,\,\, \Rightarrow {\rm{ }}\,\,\,\,\,f^\prime (t) \,=\, \left( {t^n} \right)^\prime \, =\, n{t^{n \,-\, 1}}.}</latex>
| |
| - |
| |
| - | Pravilo je: Eksponent potenčne funkcije se zmanjša za ena, prvotni pa se kot multiplikator seli pred novo potenčno funkcijo. Povsem enako pravilo velja tudi pri funkcijah necelih eksponentov.
| |
| - |
| |
| - | Sedaj pa še nedoločen integral oziroma ''F''(''t'') funkcije ''f''(''t'') = ''t''<sup>3</sup>. Funkcija ''F''(''t'') je enaka vsoti četrtine potenčne funkcije četrte stopnje in poljubne konstante:
| |
| - |
| |
| - | <latex>f(t) \,= \,{t^3}{\rm{ }} \,\,\,\,\,\Rightarrow \,\,\,\,\,{\rm{ }}F(t) \,=\, \int {f(t)} {\rm{d}}t \,=\, \int {t^3} {\rm{d}}t\, =\, \frac{t^4}{4}\, +\,C\,\,,\,\,\,\,\,{\rm{ saj \,je}}</latex>
| |
| - |
| |
| - | <latex>F^\prime (t)\, =\, \left( {\frac{t^4}{4}\, +\, C} \right)^\prime \, =\, \frac{1}{4}\left( {t^4} \right)^\prime\, +\,C^\prime \,= \,\frac{1}{4}\left( {4{t^3}} \right) \,+ \,0 \,= \,{t^3}.</latex>
| |
| - |
| |
| - | Splošno pravilo je:
| |
| - |
| |
| - | <latex>{f(t) \,=\, {t^n}\,\,,\,\,\,\,n\, \ne \, - 1{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}F(t) \,= \,\int{t^n} {\rm{d}}t \,=\, \frac{t^{n + 1}}{n\, + \,1} \,+\, C.}</latex>
| |
| - |
| |
| - |
| |
| - | '''Zgled 1'''
| |
| - | V nekem časovnem intervalu določa tok skozi tuljavo induktivnosti ''L'' izraz ''i'' = ''at''<sup>2</sup> - ''bt'' + ''c''. Izrazimo napetost na tuljavi. ⇒ Izhajamo iz enačbe tuljave:
| |
| - |
| |
| - | <latex>u\, =\, L\frac{{\rm{d}}i}{{\rm{d}}t}\, =\, Li^\prime \, =\, L(a{t^2}\, -\, bt\, +\, c)^\prime \, =\, L(2at \,-\, b).</latex>
| |
| - |
| |
| - |
| |
| - | '''Zgled 2.'''
| |
| - | Med časoma ''t''<sub>1</sub> in ''t''<sub>2</sub> podaja tok skozi upor upornosti ''R'' izraz ''i'' = ''at'' - ''b''. Izrazimo množino toplote med tema časoma. ⇒ Sproščeno toploto določa integral moči ''p'' = ''Ri''<sup>2</sup>:
| |
| - |
| |
| - | <latex>\int\limits_{t_1}^{t_2} {p{\rm{d}}t} \, =\, \int\limits_{t_1}^{t_2} {R{i^2}{\rm{d}}t}\, =\, R\int\limits_{t_1}^{t_2} {{{\left( {at \,- \,b} \right)}^2}{\rm{d}}t} \, =\, R\int\limits_{t_1}^{t_2} {\left( {{a^2}{t^2} \,- \,2abt \,+ \,{b^2}} \right){\rm{d}}t} \, =\, </latex>
| |
| - |
| |
| - | <latex>R\left( {\frac{{a^2}{t^3}}{3} \,-\, ab{t^2} \,+\, {b^2}t\, +\, C} \right)_{t_1}^{t_2}\, =\, R\left( {\frac{{a^2}t_2^3}{3} \,-\, \frac{{a^2}t_1^3}{3}\, -\, abt_2^2 \,+\, abt_1^2\, +\, {b^2}{t_2} \,-\, {b^2}{t_1}} \right).</latex>
| |
| - |
| |
| - |
| |
| - | == Harmonična funkcija ==
| |
| - |
| |
| - | Z njeno strmino, ki preide v limiti v odvod, smo se že spopadli. Takrat smo to opravili na geometrijski način, tokrat pa takole<ref>Iz matematike vemo, da je <latex>\mathop {\lim }\limits_{x \to 0} \frac{\sin x}{x}\, =\, 1.</latex></ref>:
| |
| - |
| |
| - | <latex>g(t)\, =\, \sin (\omega t\, +\, \alpha ){\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}g^\prime (t)\, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{\sin \left( {\omega (t\, +\, \Delta t) \,+\, \alpha } \right) \,-\, \sin \left( {\omega t \,+\, \alpha } \right)}{\Delta t}\, =\,</latex>
| |
| - |
| |
| - | <latex>\mathop {\lim }\limits_{\Delta t \to 0} \frac{\sin \left( {\omega t \,+\, \alpha } \right)\cos \left( {\omega \Delta t} \right)\, +\, \cos \left( {\omega t \,+\, \alpha } \right)\sin \left( {\omega \Delta t} \right) \,- \,\sin \left( {\omega t\, +\, \alpha } \right)}{\Delta t} \,=\, </latex>
| |
| - |
| |
| - | <latex> -\, \omega \sin \left( {\omega t \,+\, \alpha } \right)\mathop {\lim }\limits_{\omega \Delta t \to 0} \frac{1 \,-\, \cos \left( {\omega \Delta t} \right)}{\omega \Delta t}\, +\, \omega \cos \left( {\omega t \,+\, \alpha } \right)\mathop {\lim }\limits_{\omega \Delta t \to 0} \frac{\sin \left( {\omega \Delta t} \right)}{\omega \Delta t} \,=\, </latex>
| |
| - |
| |
| - | <latex> - \,\frac{\omega }{2}\sin \left( {\omega t\, +\, \alpha } \right)\mathop {\lim }\limits_{\omega \Delta t \to 0} \sin \left( {\omega \Delta t/2} \right)\mathop {\lim }\limits_{\omega \Delta t \to 0} \frac{\sin \left( {\omega \Delta t/2} \right)}{\omega \Delta t/2}\, +\, </latex>
| |
| - |
| |
| - | <latex>\omega \cos \left( {\omega t\, +\, \alpha } \right)\mathop {\lim }\limits_{\omega \Delta t \to 0} \frac{\sin \left( {\omega \Delta t} \right)}{\omega \Delta t}\, =\, </latex>
| |
| - |
| |
| - | <latex>\omega \cos \left( {\omega t\, +\, \alpha } \right).</latex>
| |
| - |
| |
| - | Če bi podobno postopali tudi pri kosinusni funkciji, bi dobili:
| |
| - |
| |
| - | <latex>g(t) \,=\, \sin (\omega t\, +\, \alpha ){\rm{ }} \,\,\,\,\,\Rightarrow \,\,\,\,\,{\rm{ }}g^\prime (t)\, =\, \omega \cos (\omega t\, +\, \alpha )</latex>
| |
| - |
| |
| - | <latex>f(t)\, =\, \cos (\omega t\, +\, \beta ){\rm{ }}\,\,\,\,\, \Rightarrow \,\,\,\,\,{\rm{ }}f^\prime (t)\, =\, - \omega \sin (\omega t\, +\, \beta ).</latex>
| |
| - |
| |
| - | Iz odvodov razberemo pravili. Odvod sinusne je kosinusna funkcija in odvod kosinusne je negativna sinusna funkcija. Pri odvodih se konstanta ''ω'' prenese iz argumenta v multiplikator s funkcijo. Za harmonični funkciji lahko brž najdemo še nedoločena integrala:
| |
| - |
| |
| - | <latex>g(t)\, =\, \sin (\omega t\,+\, \alpha ){\rm{ }}\,\,\,\,\, \Rightarrow \,\,\,\,\,{\rm{ }}G{\rm{(}}t{\rm{)}}\, =\, \int {\sin (\omega t\, +\, \alpha )} {\rm{d}}t \,= \, - {\omega ^{ - 1}}\cos (\omega t \,+\, \alpha ) + {C_1}</latex>
| |
| - |
| |
| - | <latex>f(t) \,=\, \cos (\omega t\, +\, \beta ){\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}F{\rm{(}}t{\rm{)}}\, =\, \int {\cos (\omega t\, +\, \beta )} {\rm{d}}t \,= \,{\omega ^{ - 1}}\sin (\omega t\, +\, \beta )\, +\, {C_2}.</latex>
| |
| - |
| |
| - |
| |
| - | '''Zgled 3'''
| |
| - | Pri analizi harmonično vzbujanih reaktivnih elementov smo ugotovili, da je moč dotekanja energije v njih harmonična časovna funkcija, katere amplituda ustreza jalovi moči ''Q''. Trenutno moč ''p''(''t'') naj določa izraz ''Q''sin(2''ωt''), v katerem je ''ω'' krožna frekvenca toka oziroma napetosti. V prvi četrtini periode toka (napetosti) je moč pozitivna in element se polni, drugo četrtino periode se element prazni itn. V trenutku ''t''<sub>0</sub> = 0 s naj bo element brez energije, ''W''(''t''<sub>0</sub>) = 0 J. Določimo energijo v elementu v kasnejšem času ''t''<sub>1</sub>. ⇒ Moč je odvod energije, zato veljajo zveze:
| |
| - |
| |
| - | <latex>\frac{{\rm{d}}W(t)}{{\rm{d}}t}\, = \,p(t){\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}W(t) \,=\, \int {p(t){\rm{d}}t} {\rm{ }} \,\,\,\,\,\Rightarrow \,\,\,\,\,{\rm{ }}W({t_1}) \,=\, W({t_0})\, +\, \int\limits_{t_0}^{t_1} {p(t){\rm{d}}t} \, =\, {\rm{ }}</latex>
| |
| - |
| |
| - | <latex>\int\limits_0^{t_1} {p(t){\rm{d}}t} \,=\, \int\limits_0^{t_1} {Q\sin (2\omega t){\rm{d}}t}\, =\, Q\left( { - \frac{\cos (2\omega t)}{2\omega }} \right)_0^{t_1} \,=\, \frac{Q}{2\omega }\left( {1 \,-\, \cos (2\omega {t_1})} \right).</latex>
| |
| - |
| |
| - | Največja energija je v elementu takrat, ko ima kosinusna funkcija vrednost -1; enaka je ''Q'' / ''ω''. Poprečna energija je polovica tega, torej ''Q'' / 2''ω''. Če ima tuljava jalovo moč 2 kvar, bo pri 50 Hz poprečna energija v njej 3,18 J, največja pa 6,36 J. Slednja je sicer majhna, vendar se moramo zavedati, da je v eni sekundi pride ali odide stokrat toliko.
| |
| - |
| |
| - |
| |
| - | == Eksponentna funkcija ==
| |
| - |
| |
| - | Zapisali jo bomo v obliki
| |
| - |
| |
| - | <latex>h(t) \,=\, {{\mathop{\rm e}\nolimits} ^{at}}.</latex>
| |
| - |
| |
| - | Matematična funkcija zahteva v argumentu neimenovano število, pri času ''t'' ima konstanta ''a'' enoto s<sup>-1</sup>. Nekaj podobnega smo zasledili pri argumentu (kotu ''ωt'') harmonične funkcije. Poiščimo odvod eksponentne funkcije<ref>Iz matematike vemo, da je <latex>\mathop {\lim }\limits_{s \to 0} {(1 + s)^{1/s}} \,=\, \mathop {\lim }\limits_{p \to \infty } {\left( {1 + 1/p}
| |
| - | \right)^p} \,=\, 1</latex></ref>:
| |
| - |
| |
| - | <latex>h(t) \,=\, {{\mathop{\rm e}\nolimits} ^{at}}\,\,\,\,\, \Rightarrow\,\,\,\,\, {\rm{ }}h^\prime (t)\, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{{{\mathop{\rm e}\nolimits} ^{a(t \,+\, \Delta t)}} \,-\, {{\mathop{\rm e}\nolimits} ^{at}}}{\Delta t}\, = \,{{\mathop{\rm e}\nolimits} ^{at}}\mathop {\lim }\limits_{\Delta t \to 0} \frac{{{\mathop{\rm e}\nolimits} ^{a\Delta t}} - 1}{\Delta t}\,= \,a{{\mathop{\rm e}\nolimits} ^{at}}\mathop {\lim }\limits_{a\Delta t \to 0} \frac{{{\mathop{\rm e}\nolimits} ^{a\Delta t}} \,- \,1}{a\Delta t}.</latex>
| |
| - |
| |
| - | Limitiranje uženemo z vpeljavo spremenljivke ''s'',
| |
| - |
| |
| - | <latex>s \,=\, {{\mathop{\rm e}\nolimits} ^{a\Delta t}}\, -\, 1{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}a\Delta t \,= \,\ln (1 \,+\, s){\rm{ }} \,\,\,\,\,\Rightarrow \,\,\,\,\,{\rm{ }}\mathop {\lim }\limits_{a\Delta t \to 0} \frac{{{\mathop{\rm e}\nolimits} ^{a\Delta t}} \,-\, 1}{a\Delta t}\, =\, \mathop {\lim }\limits_{s \to 0} \frac{s}{\ln (1 \,+ \,s)}\, =\, </latex>
| |
| - |
| |
| - | <latex>\mathop {\lim }\limits_{s \to 0} \frac{1}{{s^{ - 1}}\ln (1 \,+\, s)}\, =\, \frac{1}{\mathop {\lim }\limits_{s \to 0} {s^{ - 1}}\ln (1\, +\, s)}\, =\, \frac{1}{\ln \mathop {\lim }\limits_{s \to 0} {{(1 \,+\, s)}^{1/s}}} \,=\, \frac{1}{\ln {\mathop{\rm e}\nolimits} }\, = \,{\rm{1\,}}{\rm{,}}</latex>
| |
| - |
| |
| - | kar končno da:
| |
| - |
| |
| - | <latex>h^\prime (t)\, =\, a{\mathop{\rm e}\nolimits} ^{at}.</latex>
| |
| - |
| |
| - | Posebnost eksponentne funkcije je v tem, da se odvod in integral izražata z njo samo:
| |
| - |
| |
| - | <latex>{h(t) \,=\, {\mathop{\rm e}\nolimits} ^{at}{\rm{ }} \,\,\,\,\,\Rightarrow \,\,\,\,\,{\rm{ }}h^\prime (t)\, =\, a{\mathop{\rm e}\nolimits} ^{at}{\rm{ }}\,\,\,\,\, \Rightarrow\,\,\,\,\, {\rm{ }}H{\rm{(}}t{\rm{)}}\, =\, \int {{\mathop{\rm e}\nolimits} ^{at}} {\rm{d}}t\, =\, {a^{ - 1}}{\mathop{\rm e}\nolimits} ^{at}\, +\, C.}</latex>
| |
| - |
| |
| - |
| |
| - | '''Zgled 4'''
| |
| - | Polnilni tok kondenzatorja, ki je ob ''t''<sub>0</sub> = 0 prazen, je ''i'' = 10 mA.e<sup>-t / 2 s</sup>; ''Q''(''t''<sub>0</sub>) = 0 C. Ob ''t''<sub>0</sub> = 0 je jakost toka 10 mA, po dveh sekundah 10 mA / e, po štirih 10 mA / e<sup>2</sup>, po šestih 10 mA / e<sup>3</sup>, po 10 s pa komaj še 10 mA / e<sup>5</sup> ≅ 0,067 mA, kar ustreza komaj 2/3 % začetnega toka. Izračunajmo naboj, ki priteče na ploščo do 10 sekunde. ⇒ Račun je podoben prejšnjemu. Tok je odvod naboja:
| |
| - |
| |
| - | <latex>\frac{{\rm{d}}Q(t)}{{\rm{d}}t}\, =\, i(t){\rm{ }} \,\,\,\,\,\Rightarrow \,\,\,\,\,{\rm{ }}Q(t)\, =\, \int {i(t){\rm{d}}t} {\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}Q({t_1}) \,=\, Q({t_0}) \,+\, \int\limits_{t_0}^{t_1} {i(t){\rm{d}}t} \, =\, </latex>
| |
| - |
| |
| - | <latex>\int\limits_{t_0}^{t_1} {i(t){\rm{d}}t} \,=\, {10^{ - 2}}{\rm{ A}} \,\cdot\, \int\limits_0^{10{\rm{ s}}} {{{\rm{e}}^{ - t/2{\rm{ s}}}}{\rm{d}}t} \,=\, {10^{ - 2}}{\rm{ A}} \,\cdot \,\left( { - \frac{{\rm{e}}^{ - t/2{\rm{ s}}}}{1/2{\rm{ s}}}}\right)_0^{10{\rm{ s}}}\, =\, 20{\rm{ mC}} \,\cdot\, \left( {1\, -\, {{\rm{e}}^{ - 5}}} \right)\, \cong\, 19,87\,{\rm{ mC}}.</latex>
| |
| - |
| |
| - | Po zelo (zelo) dolgem času bo naboj dosegel vrednost 20 mC.
| |
| - |
| |
| - |
| |
| - | <references />
| |
| | | | |
| | {{Hierarchy footer}} | | {{Hierarchy footer}} |