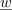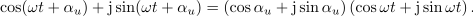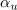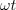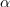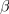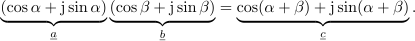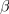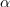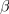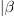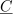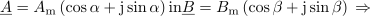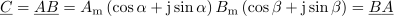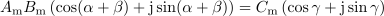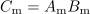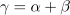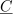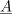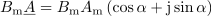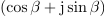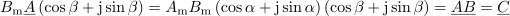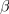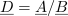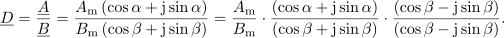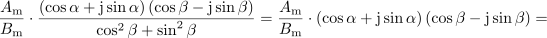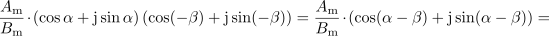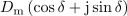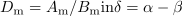Iz e-ELEKTROTEHNIKA plus
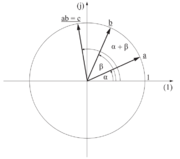
Slika 18: Produkt enotinih kazalcev predstavimo grafično z zavrtitvijo enega za kot drugega v pozitivni smeri.
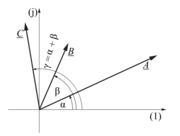
Slika 19: Produkt kazalcev predstavimo grafično z zavrtitvijo prvega za kot drugega v pozitivni smeri in z množenjem z absolutno vrednostjo drugega.
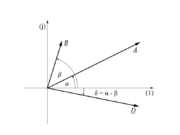
Slika 20: Kvocient kazalcev predstavimo grafično z zavrtitvijo prvega za kot drugega v desno in z deljenjem tega z absolutno vrednostjo drugega.
V izvajanju, ki je vodilo k vpeljavi kazalca, smo pri preoblikovanju funkcije
prišli do zveze:
Leva stran je kazalec, ki je enak produktu dveh kazalcev. Pomena kotov
in
za samo zvezo nista pomembna; zamenjajmo ju s kotoma
in
:
Argument desnega kazalca je enak vsoti argumentov levih dveh, absolutne vrednosti vseh treh kazalcev pa so enake 1 (slika 18); zaključimo lahko, da je produkt operacija, ki vključuje vrtenje. Produktni kazalec pridobimo tako, da prvega zavrtimo v levo za kot
, ali pa drugega v isto smer za kot
. Če je kot
npr. negativen, pomeni, da je potrebno prvi kazalec zavrteti za
v desno.
Nekaj podobnega ugotavljamo tudi za produktni kazalec
kazalcev
in
:
.
Iz primerjave izrazov sledi:
in
.
Kazalec
dobimo tako, da množimo npr. kazalec
z
, dobimo kazalec
,
nato pa tega množimo še s
:
,
da se zavrti za kot
v pozitivni smeri (slika 19).
Zelo podobno je pri deljenju kazalcev. Za kazalec
pišemo:
Števec in imenovalec smo množili s konjugiranim imenovalcem, dobimo:
.
Iz primerjave izrazov sledi:
.
Kvocient dveh kazalcev je spet kazalec; grafično ga dobimo tako, da prvega delimo z absolutno vrednostjo drugega in ga zavrtimo v nasprotni smeri za kot drugega kazalca (slika 20).