6.6 Druga nihajna vezja

Iz e-ELEKTROTEHNIKA plus

Vzporedni in zaporedni nihajni krog sta osnovni in za analizo najpreprostejši nihajni vezji, nikakor pa ne edini. Navidez preprosto vezje zaporedne vezave upora in tuljave in njej vzporednega kondenzatorja in upora (pomeniti more nadomestno vezje realnega nihajnega kroga, ki ga oblikujeta realna tuljava in realen kondenzator) je že zahtevnejši primer (slika 56). Izrazimo impedanco vezja, njeno absolutno vrednost in argument:

,

.

Pri vzbujanju dvopola z napetostnim virom nastavljive frekvence nastopi tokovna resonanca pri frekvenci, pri kateri je absolutna vrednost impedance najmanjša. Njeno vrednost najdemo numerično, in sicer tako, da funkcijo tabeliramo (narišemo) in iz nje izčitamo približno vrednost frekvence, pri kateri ima krivulja minimum.

Druga pot določitve resonančne frekvence je sicer analitična, vendar približna: opira se na izkušnjo, da je fazni kot za osnovni nihajni vezji v resonanci enak nič. Če bi to uveljavili v tem vezju, bi za frekvenco , pri kateri je fazni kot enak nič, dobili tole:

.

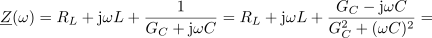
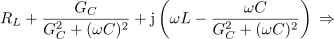
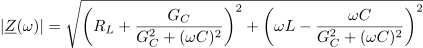
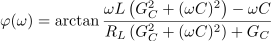
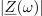
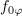
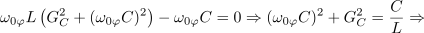
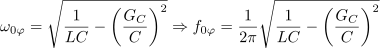
Po tej formuli izračunana frekvenca ni povsem prava resonančna frekvenca, se pa izkaže, da je zelo blizu nje. Pri tej frekvenci je impedanca nihajnega vezja realna:

.

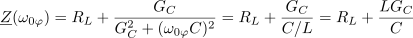
Tok vira in in napetost nihajnega vezja sta v fazi; vezje se pri tej frekvenci vede kot upor. Energija, ki izhaja iz vira, se pretvarja v toploto v uporih, med kondenzatorjem in tuljavo pa se izmenjuje enaka množina energije.

6.5 Uporaba napetostne resonance

7 Trifazni sistemi (višji nivo)