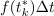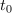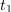5.4 Določen integral funkcije

Iz e-ELEKTROTEHNIKA plus

Slika 93: Upodobitev vsote

sumandov

s površino niza ozkih trakov, ležečih med krajnima trenutkoma

in

.

Slika 94: Vrednost določenega integrala funkcije

med

in

je sorazmerna površini osenčenega lika med krivuljo in abscisno osjo.

Za razumevanje določenega integrala funkcije je najbolje, če imamo pred očmi fizikalni primer. 1) V element vezja naj priteka energija z močjo p(t). V času Δt vstopi vanj energijski paket pΔt. Ker je moč v splošnem spremenljiva, bodo energijski paketi v sledečih časih Δt različni. Če želimo ugotoviti energijo, ki je vstopila v element, je potrebno energijske pakete sešteti. 2) Naj bo i(t) funkcija, ki podaja polnilni tok. V času Δt se plošči kondenzatorjev obogatita z elektrinama ±iΔt, napetost pa s prirastkom iΔt / C. Ker je polnilni tok v splošnem vsak trenutek drugačen, so v kasnejših časih Δt takšni tudi paketi elektrine in enako tudi prirastki napetosti. Če seštejemo vse prirastke napetosti, dobimo vrednost, za katero se je spremenila napetost kondenzatorja. Primera zastavljata nalogo: sešteti določene majhne vrednosti dane količine, pri tem pa pridobiti čim točnejši rezultat.

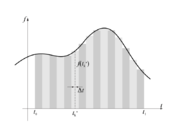
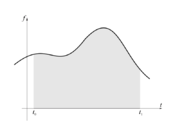
Zapustimo moč (tok) in pakete energije (naboja) in se raje posvetimo splošni časovni funkciji, ki naj je za začetek pozitivna, f(t) > 0, ter njenim »paketom« in vsoti teh znotraj intervala t ∈ [t₀, t₁] (slika 93). (V primeru moči bi vsota pomenila energijo, ki je prispela v element, v primeru toka pa elektrino, ki je pritekla na ploščo.) Interval [t₀, t₁] razdelimo na n podintervalov trajanja Δt = (t₁ - t₀) / n. »Jakost« f(t_k^*)Δt k-tega »paketa« ustreza »ploščini« pravokotnika s stranicama Δt in f(t_k^*), pri čemer je t_k^* trenutek v k-tem podintervalu, vsota

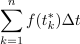
pa ustreza površini vseh takšnih pravokotnikov med t₀ in t₁^[1]. Če bi za čase t_k^* izbrali čase (t_k^s) najmanjših funkcijskih vrednosti funkcije, bi za vsoto dobili vrednost S_n, če pa bi zatem za čase t_k^* izbirali čase (t_k^z) največjih funkcijskih vrednosti funkcije v podintervalih, bi za vsoto dobili vrednost Z_n. Slednja je gotovo večja ali kvečjemu enaka prejšnji vrednosti vsote:

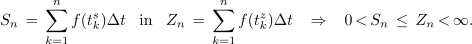
Z nekaj premalo (S_n) ali z nekaj preveč (Z_n) verjetno nismo zadovoljni, razen če smo praktični in se zadovoljimo s približnim rezultatom, kar seveda tudi ne gre zavreči. Prepričani smo, da bo najbolj prava vrednost I, ki jo imenujemo določen integral funkcije f(t) na intervalu [t₀, t₁], nekje med vrednostma S_n in Z_n, S_n ≤ I ≤ Z_n. Vrednosti I se bo vsota S_n približala z leve, vsota Z_n pa z desne strani, če bo le število n kar največje, stremeče v neskončnost. Vsoti, v kateri število sumandov (n) prekaša vse meje, rečemo izlimitirana vsota, in pišemo:

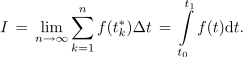
Integracijski znak »∫« zamenjuje sumacijski znak »∑«, meji seštevanja, t₀ in t₁ zamenjujeta skrajni vrednosti sumacijskega indeksa k in infinitezimalni paket f(t)dt zamenjuje majhen paket f(t_k^*)Δt^[2]. (Če bi funkcija f pomenila električni tok (ali moč), bi integral I pomenil v tem času pretečen naboj (ali energijo).)

Glede na to, da smo sumande vsot interpretirali s ploščinami pravokotnikov, bi utegnili določen integral interpretirati s »površino« lika med abscisno osjo in funkcijo na intervalu [t₀, t₁] (slika 94). Določen integral ima nekaj lepih lastnosti. 1) Če je na integracijskem intervalu funkcija g A-kratnik funkcije f, je integral funkcije g A-kratnik integrala funkcije f. 2) Če je na integracijskem intervalu funkcija f negativna, ima negativno vrednost tudi določen integral. 3) Če ima določen integral funkcije f od t₀ do t₁ vrednost I, vrednost J pa od t₁ do t₂, potem ima določen integral funkcije f od t₀ do t₂ vrednost I + J:

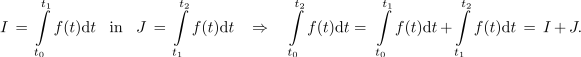
Primer. Če je tok med prvo in tretjo sekundo prenesel naboj 1 μC, med tretjo in enajsto sekundo pa naboj -3 μC, potem je med prvo in enajsto sekundo ta tok prenesel naboj -2 μC.

Opombe

1. ↑ Ploščino pravokotnika smo postavili med navednici in se s tem zavarovali: da ne govorimo o ploščini oziroma kvadraturi lika (saj stranici nimata dolžinskega značaja), ampak o produktu, ki ga je - v določenem merilu - mogoče interpretirati s površino pravokotnika.
2. ↑ Integralu rečemo tudi zvezna vsota, za razliko od vsote, ki predstavlja diskretno seštevanje.

Podpoglavja:

• 5.4.1 Določen integral kot funkcija zgornje meje
• 5.4.2 Odvod funkcije zgornje meje določenega integrala

5.3.1 Časovni odvodi in diferenciali v elektrotehniki

5.4.1 Določen integral kot funkcija zgornje meje