5.6 Zveza med določenim in nedoločenim integralom

Iz e-ELEKTROTEHNIKA plus

Če smo našli funkcijo F, katere odvod je f, je z njo določena funkcija G. Določena je vrednost G(t₁) in tudi vrednost določenega integrala I, s katerim smo integriranje začeli:

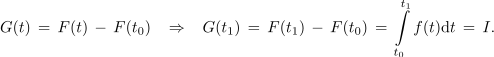
Od funkcije G, ki nam je veliko pomagala, se sedaj »poslovimo« in sklenimo:

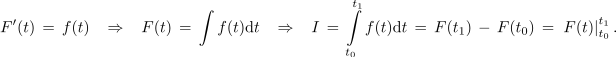
Določen integral I funkcije f na intervalu [t₀, t₁] izračunamo tako, da najdemo funkciji f njen nedoločen integral F, zatem pa tvorimo še razliko funkcijskih vrednosti funkcije F na zgornji in na spodnji integracijski meji.

5.5 Nedoločen integral funkcije

5.7 Odvodi in integrali nekaterih elementarnih funkcij