Iz e-ELEKTROTEHNIKA plus
Ali znamo reči kaj o odvodu funkcije G v točki t* oziroma o limiti naslednjega kvocienta:
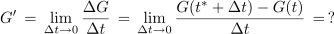
Iz lastnosti integrala izhaja, da je števec v resnici določen integral funkcije f od t* do t* + Δt, saj je
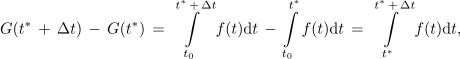
in da je iskan odvod možno izraziti takole:
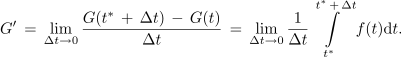
Preostali določen integral se naslavlja na kar najkrajši interval Δt; če je tako, ustreza približni vrednosti integrala morda že kar produkt f(t* + Δt) Δt, če je le Δt dovolj majhen. Sledi odgovor:
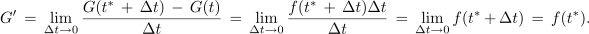
Odvod funkcije G v t* je enak funkcijski vrednosti funkcije f v t*, pri tem pa je t* ∈ [t0, t1]. Izkoristimo priliko in izpostavimo glavne lastnosti določnega integrala kot funkcije zgornje meje:
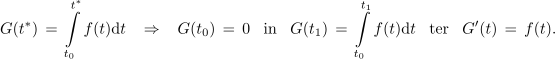
| | 5.5 Nedoločen integral funkcije |
