Test

Iz e-ELEKTROTEHNIKA plus

(Primerjava redakcij)

Skoči na: navigacija, iskanje

Redakcija: 19:34, 31. avgust 2010

Preizkusi znanje

Rešeni primer 1

0

Rešeni primer 1
Izračunaj trenutno vrednost sinusne izmenične napetosti v času t = 0,00167 s. Njena maksimalna vrednost je 180 V, začetni fazni kot napetosti je 0 °, frekvenca pa 50 Hz.
2
Fazni kot napetosti v času 0,00167 s je: α =
30
º.
Ker je trenutna napetost odvisna od trenutnega faznega kota napetosti, izračunamo fazni kot napetosti v času 0,00167 s. Pri izračunu dobimo kot v radianih, ki ga nato pretvorimo v stopinje.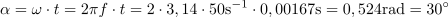

Trenutna vrednost napetosti v času t = 0,00167 s je: u =
90
V.
Trenutna napetost je določena z maksimalno napetostjo in trenutnim faznim kotom. Na trenutni fazni kot vpliva tudi začetni fazni kot, zato ga upoštevamo. V našem primeru je 0º, zato ne spreminja poteka napetosti. Zagotoviti moramo, da oba kota, ki nastopata v enačbi, izrazimo na enak način, v stopinjah ali radianih.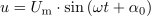

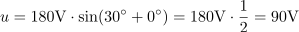1. odgovor
2.
0
0
0
0

Namig

dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 2

0

Rešeni primer 2
Trenutni vrednosti napetosti na dveh zaporedno vezanih uporih se spreminjata po enačbah u₁ = 110 ∙ sin (314t) V in u₂ = 113 ∙ sin (314t) V. Določi maksimalno vrednost vsote napetosti, efektivno vrednost in napiši enačbo za trenutno vrednost vsote napetosti.
3
Maksimalna napetost vsote napetosti na obeh zaporedno vezanih uporih je: U_m=
223
V.
Ker imata napetosti na obeh zaporedno vezanih uporih enako spreminjanje faznega kota (sta v fazi in imata enako frekvenco), je maksimalna napetost vsote napetosti enaka vsoti maksimalnih napetosti na posameznih uporih.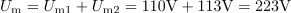

Efektivna vrednost vsote napetosti na obeh uporih je: U =
157.7
V.
Pri sinusnem poteku izmenične napetosti je efektivna vrednost napetosti za

-krat manjša v primerjavi z maksimalno napetostjo.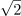

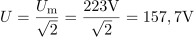Enačba za trenutno vrednost vsote napetosti na obeh uporih je: u =
223
∙ sin (314t) V.
Enačbo trenutne napetosti določa maksimalna napetost vsote napetosti in trenuten fazni kot napetosti.

1. odgovor
2.
3.
0
0
0
0
0
0

Namig

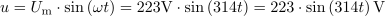dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 3

0

Rešeni primer 3
Izračunaj frekvenco sinusne izmenične napetosti, ki po 5 ms doseže trenutno vrednost 15 V, če je njena maksimalna vrednost 20 V in začetni fazni kot 30 °.
5
Sinus trenutnega kota znaša: sinαt =
0.75
.
Na osnovi razmerja med trenutno in maksimalno vrednostjo napetosti lahko izračunamo sinus trenutnega faznega kota, ki nas bo pripeljal do določitve trenutnega kota.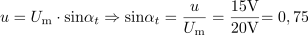

Trenutni fazni kot izmenične napetosti je: αt =
0.85
rad.
Ker poznamo sinusno vrednost trenutnega faznega kota, lahko določimo tudi trenutni fazni kot napetosti.

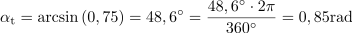V 5 ms se je fazni kot spremenil za: α =
0.314
rad.
Z upoštevanjem začetnega faznega kota α₀ in trenutnega faznega kota αt določimo spremembo faznega kota α po 5 ms.

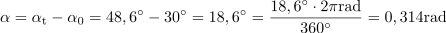Krožna frekvenca izmenične sinusne napetosti je: ω =
62.8
rad/s.
Iz znane spremembe faznega kota α in časa t izračunamo krožno frekvenco ω.

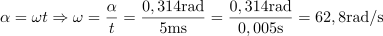Frekvenca sinusne izmenične napetosti je: f =
10
Hz.
Ker poznamo krožno frekvenco ω, lahko izračunamo frekvenco sinusne izmenične napetosti f, saj je med njima faktor 2π.

1. odgovor
2.
3.
4.
5.
0
0
0
0
0
0
0
0
0
0

Namig

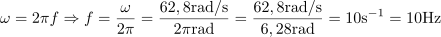dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 4

0

Rešeni primer 4
Trenutna vrednost sinusne izmenične napetosti s frekvenco 50 Hz je 96,6 V, njena maksimalna vrednost pa 100 V. V kolikšnem času doseže napetost prvič podano trenutno vrednost, če je začetni fazni kot -30 °?
4
V času trenutne napetosti 96,6 V je sinus trenutnega kota α_t: sin α_t =
0.966
.
Ker poznamo trenutno in maksimalno vrednost sinusne izmenične napetosti, lahko iz njunega razmerja določimo sinus trenutnega kota.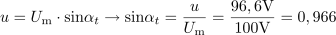

Trenutni fazni kot izmenične sinusne napetosti je: α_t =
75
°.
Ker poznamo sinus trenutnega kota, lahko izračunamo pripadajoč kot.

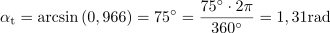V času t se je fazni kot spremenil za: α =
105
°.
Z upoštevanjem trenutnega faznega kota α_t in njegove začetne vrednosti α₀ lahko določimo spremembo faznega kota α v času t.

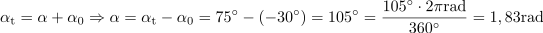Sinusna izmenična napetost doseže trenutno vrednost napetosti pri frekvenci 50 Hz, začetnem faznem kotu -30 º in amplitudi 100 V v času: t =
5.8
ms.
Ker poznamo spremembo faznega kota in frekvenco sinusne izmenične napetosti f, lahko izračunamo čas t, v katerem se je fazni kot spremenil za 105 º (1,83 rad) oziroma je napetost zavzela trenutno vrednost 96,6 V.

1. odgovor
2.
3.
4.
0
0
0
0
0
0
0
0

Namig

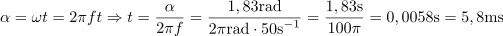dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 5

0

Rešeni primer 5
Sinusno izmenična napetost s frekvenco 100 Hz in z maksimalno vrednostjo 100 V ima začetni fazni kot α₀ = -30 °. Izračunaj efektivno vrednost napetosti in določi periodo.
2
Efektivna vrednost sinusne izmenične napetosti s frekvenco 100 Hz, z maksimalno vrednostjo 100 V in začetnim faznim kotom α₀ = -30 ° je: U =
70.7
V.
Za predstavitev efektivne vrednosti sinusne izmenične napetosti v časovnem diagramu izračunamo njeno velikost iz maksimalne napetosti, saj gre za periodičen pojav.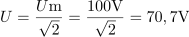

Perioda sinusne izmenične napetosti s frekvenco 100 Hz je: T =
10
ms.
Perioda izmeničnega signala je obratnosorazmerna s frekvenco signala, kar upoštevamo pri izračunu periode.

1. odgovor
2.
0
0
0
0

Namig

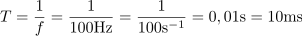dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 6

0

Rešeni primer 6
V časovnem diagramu nariši dve sinusni izmenični napetosti tako, da bo začetni fazni kot prve 45 °, u₂ pa zaostaja za u₁ za 90 °. Obe napetosti imata enako amplitudo 1 V.
2
0
Časovni diagram, ki prikazuje potek napetosti v odvisnosti od časa, pripravimo tako, da x os opremimo s faznim kotom ωt in enotami kota v radianih od 0 do 3π, kar zadošča za prikaz ene in pol periode signala. Na y osi pa je trenutna napetost od -1 V do +1 V z ločljivostjo 0,2 V. Ker je začetni fazni kot napetosti u₁ 45 º, to pomeni, da ima napetost v izhodišču diagrama že tolikšno vrednost kot bi jo sicer imela pri faznem kotu 45 º, oziroma, da napetost seka x os že pri faznem kotu -45 º (-π/4), naslednjič pa pri faznem kotu 3π/4 radianov.
0
Ker napetost u₂ zaostaja za u₁ za 90 º, bo njen potek pomaknjen v desno za fazni kot 90 º oziroma za π/2 radianov. Če seka u₁ x os pri kotu -45 º (-π/4), pa seka u₂ x os šele pri kotu +45 º (+π/4), ker zaostaja za 90 º.
1. odgovor
2.
0
0
0
0

Namig

dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 7

0

Rešeni primer 7
Nariši kazalčni diagram napetosti in toka tako, da bo začetni fazni kot napetosti -45 °, tok i pa prehiteva napetost u za 60 °.
2
0
Za boljšo predstavo si narišemo koordinatni sistem, pri katerem predstavlja ničelni fazni kot pozitivni del x osi. En obhod v kazalčnem diagramu pomeni zasuk za 360 º oziroma za 2π radianov. V diagram vrišemo kazalec napetosti z oznako U_m, ki se nahaja 45 º pred ničelnim kotom oziroma na polovici kvadranta pod x osjo. Njegov položaj določa kot α = - 45 º.
0
Kazalcu U_m dodamo še kazalec toka I_m, ki prehiteva kazalec napetosti za 60 º v smeri, ki je nasprotna vrtenju kazalcev na uri. Lahko rečemo, da napetost zaostaja za tokom ali da tok prehiteva napetost. Med njima je fazni kot φ.
1. odgovor
2.
0
0
0
0

Namig

dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 8

0

Rešeni primer 8
Napetosti u₁ in u₂ sta podani s kazalčnim diagramom. Določi začetni fazni kot vsake od napetosti in fazni kot med njima. Vse kote zapiši v stopinjah. Ugotovi ali napetost u₂ prehiteva ali zaostaja za napetostjo u₁.
3
Izhodiščni fazni kot napetosti u₁ je: α_0u1 =
90
°.
Začetni fazni kot napetosti u₁ predstavlja kot med pozitivnim delom x osi koordinatnega sistema in kazalcem U_1m. Pozitivno smer vrtenja kazalcev predstavlja smer, ki je nasprotna smeri vrtenja kazalcev na uri, kar upoštevamo pri določitvi začetnega faznega kota u₁.
Ker leži kazalec napetosti U_1m za izhodiščem v smeri vrtenja, je začetni fazni kot napetosti u₁ pozitiven. Kot med izhodiščem in kazalcem U_1m predstavlja četrtino kroga oziroma 90 º (π/2), zato je začetni fazni kot α_0u1 = 90 º.
Izhodiščni fazni kot napetosti u2 je: α_0u2 =
-90
°.
Tudi začetni kot napetosti u2 določimo glede na kot med pozitivnim delom x osi koordinatnega sistema in kazalcem U_2m. Kazalec se nahaja pred izhodiščem, torej v smeri vrtenja urinih kazalcev, kar predstavlja negativno smer, zato je začetni fazni kot negativen.
Kazalec U_2m oklepa z izhodiščem kot 90 º. Ker se kazalec nahaja pred izhodiščno smerjo, je začetni fazni kot negativen, torej α_0u2 = -90 º.
Fazni kot med napetostjo u₁ in u₂ je: φ =
180
°.
Fazni kot med napetostima izračunamo kot razliko začetnih faznih kotov, seveda le pri pogoju, da je frekvenca obeh napetosti enaka.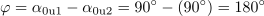

Napetost u₁ prehiteva napetost u₂ za 180 º.
1. odgovor
2.
3.
0
0
0
0
0
0

Namig

dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 9

0

Rešeni primer 9
Ohmski upor z upornostjo 40 Ω je priključen na sinusno napetost, ki se spreminja po enačbi u = 169,2 ∙ sin(314t) V. Izračunaj efektivno vrednost napetosti in toka ter moč na uporu. Določi tudi frekvenco in periodo toka ter napetosti, pa tudi delovno energijo, ki se na uporu porabi v 5 urah. Napiši tudi enačbo za trenutno vrednost toka.
7
Efektivna napetost, na katero je priključen upor, je: U =
120
V.
Ker poznamo enačbo, ki opisuje spreminjanje napetosti (trenutna napetost), iz katere lahko razberemo tudi podatek o maksimalni napetosti, lahko na tej osnovi izračunamo efektivno napetost.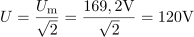

Skozi ohmski upor teče efektivni tok: I =
3
A.
Za izračun efektivnega toka skozi ohmski upor uporabimo Ohmov zakon.

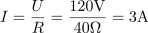Na ohmskem uporu se sprošča delovna moč: P =
360
W.
Moč na ohmskem uporu določata efektivna napetost in efektivni tok.

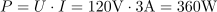V petih urah se na ohmskem uporu sprosti delovna energija: W =
1.8
kWh.
Na uporu se sprošča delovna energija, ki je odvisna od moči in časa, ko je prisotna moč.

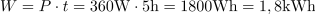Frekvenca izmenične napetosti (in toka) na ohmskem uporu je: f =
50
Hz.
Pri izračunu frekvence izhajamo iz krožne frekvence ω, ki jo razberemo iz enačbe za trenutno napetost u. Napetost poganja tok, ki teče skozi omski upor, zato imata tok in napetost enako frekvenco.

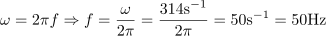Perioda izmenične napetosti in toka je: T =
20
ms.
Ker poznamo frekvenco napetosti in toka, lahko izračunamo tudi periodo za ti dve veličini.

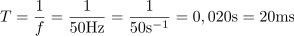Maksimalna vrednost toka skozi ohmski upor je: I_m =
4.23
A.
Enačba za trenutno vrednost toka skozi upor ima obliko: i = 4,23 ∙ sin(314t) A.
Ker poznamo enačbo za trenutno napetost, lahko določimo tudi enačbo za trenutni tok. Seveda moramo prej izračunati maksimalni tok.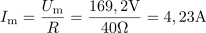

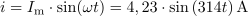1. odgovor
2.
3.
4.
5.
6.
7.
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Namig

dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 10

0

Rešeni primer 10
Ohmski upor z upornostjo 40 Ω priključimo enkrat na sinusno, drugič pa na pravokotno napetost. V obeh primerih je velikost maksimalne napetosti 12 V. Izračunaj delovno moč na uporu za sinusno in za pravokotno napetost.
4
Efektivna napetost na uporu pri sinusni obliki napetosti je: U =
8.5
V.
Za izračun delovne moči na uporu moramo poznati efektivno vrednost napetosti in ohmsko upornost, zato najprej izračunamo efektivno napetost za sinusno obliko napetosti.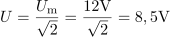

Pri sinusni obliki napetosti se na ohmskem uporu sprošča delovna moč: P =
1.81
W.
Moč na ohmskem uporu je odvisna od kvadrata napetosti in ohmske upornosti.

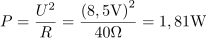Efektivna napetost na uporu pri pravokotni obliki napetosti je: U =
12
V.
Pri pravokotni obliki napetosti se napetost spreminja s časom le po smeri, ne pa po velikosti, kar vpliva na velikost efektivne vrednosti.

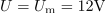Pri pravokotni obliki napetosti se na ohmskem uporu sprošča delovna moč: P =
3.6
V.
Moč na ohmskem uporu izračunamo pri pravokotni obliki napetosti na enak način kot pri sinusni obliki napetosti.

1. odgovor
2.
3.
4.
0
0
0
0
0
0
0
0

Namig

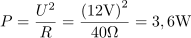dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 11

0

Rešeni primer 11
Izračunaj induktivno impedanco tuljave z induktivnostjo L = 25,5 mH pri dveh različnih frekvencah 50 Hz in 400 Hz. Kolikšen je v obeh primerih efektivni tok in kolikšna jalova moč, če je tuljava priključena na napetost 120 V in če zanemarimo ohmsko upornost navitja?
6
Pri frekvenci 50 Hz je induktivna upornost tuljave: X_L1 =
8
Ω.
Za izračun jalove moči moramo poleg efektivne napetosti, na katero je priključena tuljava, poznati tudi impedanco tuljave, ki jo določata frekvenca in induktivnost tuljave.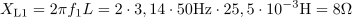

Pri frekvenci 50 Hz teče skozi tuljavo induktivni jalov tok: I₁ =
15
A.
Induktivni jalov tok skozi tuljavo, ki zaostaja za napetostjo za 90 º, izračunamo po Ohmovem zakonu, ker poznamo efektivno napetost in induktivno upornost tuljave.

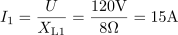Pri frekvenci 50 Hz je jalova moč, ki se prenaša med generatorjem in tuljavo: Q_L1 =
1800
var.
Produkt napetosti na tuljavi in induktivnega jalovega toka skozi tuljavo določa jalovo moč.

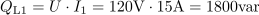Pri frekvenci 400 Hz je induktivna upornost tuljave: X_L2 =
64
Ω.
Pri frekvenci 400 Hz ima tuljava pri nespremenjeni induktivnosti višjo induktivno upornost, saj je le-ta odvisna od frekvence.

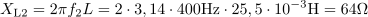Tok skozi tuljavo omejuje induktivna upornost pri frekvenci 400 Hz na: I₂ =
1.87
A.
Ker se je zararadi višje frekvence povečala induktivna upornost, se posledično zmanjša induktivni jalov tok skozi tuljavo.

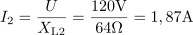Jalova moč na tuljavi znaša pri frekvenci 400 Hz: Q_L2 =
224
var.
Zaradi zmanjšanega induktivnega jalovega toka pri nespremenjeni napetosti je tudi jalova moč manjša.

1. odgovor
2.
3.
4.
5.
6.
0
0
0
0
0
0
0
0
0
0
0
0

Namig

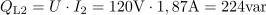dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 12

0

Rešeni primer 12
Tuljava z induktivnostjo 35 mH in zanemarljivo ohmsko upornostjo je priključena na izmenično napetost u = 310 ∙ sin(314t + 90 °). Kolikšna je efektivna vrednost napetosti in kolikšna induktivna upornost tuljave? Kolikšen tok pokaže ampermeter? Izračunaj induktivno jalovo moč in zapiši enačbo za trenutno vrednost toka.
5
Efektivna vrednost napetosti na tuljavi je: U =
220
V.
Efektivno vrednost napetosti izračunamo iz maksimalne napetosti, ki jo najdemo v enačbi za trenutno napetost.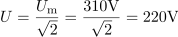

Induktivna upornost tuljave je: X_L =
11
Ω.
Za izračun induktivne upornosti potrebujemo frekvenco napetosti, kjer si spet pomagamo z enačbo trenutne napetosti, in induktivnost tuljave.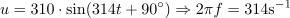

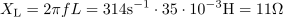Efektivni tok, ki ga izmeri ampermeter, je: I_L =
20
A.
Ampermeter meri efektivni tok skozi tuljavo in je po Ohmovem zakonu odvisen od efektivne napetosti in induktivne upornosti tuljave.

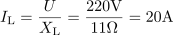Induktivna jalova moč znaša: Q_L =
4.4
kvar.
Pri znani efektivni napetosti in znanem efektivnem induktivnem jalovem toku skozi tuljavo izračunamo iz njunega zmnožka induktivno jalovo moč.

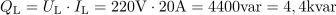Enačbo, ki opisuje trenutno vrednost induktivnega jalovega toka, zapišemo kot: i =
28.2

.
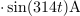Enačbo za trenutno vrednost toka izpeljemo iz enačbe za trenutno vrednost napetosti, če upoštevamo induktivno upornost, ki omejuje tok skozi tuljavo. Pri tem se zavedamo, da induktivni jalov tok zaostaja za napetostjo za 90 º.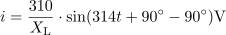

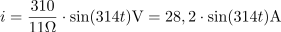1. odgovor
2.
3.
4.
5.
0
0
0
0
0
0
0
0
0
0

Namig

dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 13

0

Rešeni primer 13
Tuljava z induktivnostjo 50 mH (ohmsko upornost zanemarimo) je priključena na napetost 200 V. Kolikšna je frekvenca priključene napetosti, če je induktivna jalova moč 500 var?
3
Vrednost efektivnega induktivnega jalovega toka skozi tuljavo je: I =
2.5
A.
Iz enačbe za induktivno jalovo moč lahko izračunamo induktivni jalov tok pri podani napetosti, da bi nato mogli priti do induktivne upornosti in preko nje do frekvence napetosti.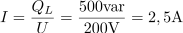

Induktivna upornost znaša: X_L =
80
Ω.
Po Ohmovem zakonu dobimo induktivno upornost iz razmerja med napetostjo in tokom.

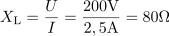Frekvenca napetosti, na katero je priključena tuljava, je: f =
255
Hz.
Frekvenco lahko izrazimo iz enačbe za induktivno upornost, saj poznamo vse ostale veličine.

1. odgovor
2.
3.
0
0
0
0
0
0

Namig

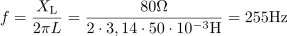dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 14

0

Rešeni primer 14
Kondenzator s kapacitivnostjo 8 μF je priključen na sinusno napetost 12 V frekvence 500 Hz. Kolikšen tok teče v tokokrogu?
2
Kapacitivna upornost kondenzatorja pri 500 Hz je: X_C =
39.8
Ω.
Kondenzator ima v izmeničnem krogu kapacitvino upornost, ki določa kapacitivni jalov tok, zato jo izračunamo najprej.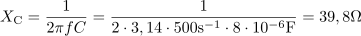

V tokokrogu teče kapacitivni jalov tok: I =
0.3
A.
Kapacitivni jalov tok, ki teče skozi kondenzator, izračunamo po Ohmovem zakonu.

1. odgovor
2.
0
0
0
0

Namig

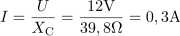dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 15

0

Rešeni primer 15
Kondenzator s kapacitivnostjo 318 μF je priključen na izmenično napetost 120 V frekvence 50 Hz. Izračunaj tok skozi kondenzator in kapacitivno jalovo moč.
3
Kapacitivna upornost kondenzatorja pri frekvenci 50 Hz je: X_C =
10
Ω.
Za izračun toka skozi kondenzator moramo poznati njegovo kapacitivno upornost pri podani frekvenci.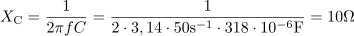

Pri frekvenci 50 Hz teče v tokokrogu tok: I =
12
A.
V tokokrogu s kondenzatorjem teče kapacitivni jalov tok, ki ga določata pritisnjena napetost in kapacitivna upornost kondenzatorja.

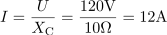Kapacitivna jalova moč znaša: Q_C =
1440
var.
Kapacitivno jalovo moč, ki se prenaša v tokokrogu, lahko izračunamo iz napetosti in kapacitivne upornosti, toka in kapacitivne upornosti ali pa iz toka in napetosti.

1. odgovor
2.
3.
0
0
0
0
0
0

Namig

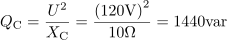dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 16

0

Rešeni primer 16
Kondenzator s kapacitivnostjo 20 μF je priključen na izmenično napetost u = 169 ∙ sin(628t) V. Izračunaj kapacitivno upornost, efektivno vrednost toka in zapiši enačbo za trenutno vrednost toka.
4
Kondenzator s kapacitivnostjo 20 μF ima kapacitivno upornost: X_C =
80
Ω.
Iz znanih podatkov lahko izračunamo kapacitivno upornost konenzatorja, ki jo uporabimo za izračun toka. Podatek o krožni frekvenci ω najdemo v enačbi za trenutno napetost u.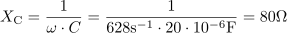

Maksimalna vrednost toka je: I_m =
2.1
A.
Maksimalno vrednost toka izračunamo iz maksimalne napetosti in kapacitvne upornosti po Ohmovem zakonu.

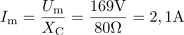Pri maksimalnem toku 2,1 A ima efektivni tok velikost: I =
1.5
A.
Pri sinusnem poteku toka je faktor med maksimalno in efektivno vrednostjo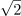

.

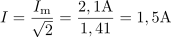Trenutno vrednost toka v tokokrogu zapišemo z enačbo: i =
2.1
∙ sin(628t + 90 º) A.
Enačbo za trenutno vrednost toka dobimo iz enačbe za trenutno vrednost napetosti, saj je frekvenca obeh veličin enaka, upoštevati pa moramo fazni kot med tokom in napetostjo in maksimalni tok, ki smo ga že določili.

1. odgovor
2.
3.
4.
0
0
0
0
0
0
0
0

Namig

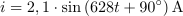dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 17

0

Rešeni primer 17
Ohmski upor z ohmsko upornostjo 30 Ω in tuljava z induktivnostjo 127 mH sta vezana zaporedno in priključena na sinusno napetost frekvence 50 Hz. Maksimalna vrednost toka je 6,2 A, začetni fazni kot pa 0 °. Izračunaj efektivne vrednosti napetosti na uporu in tuljavi ter priključno napetost generatorja. Določi tudi navidezno in delovno moč generatorja.
9
Na ohmskem uporu je maksimalna napetost: U_Rm =
186
V.
Ker poznamo maksimalni tok v tokokrogu in ohmsko upornost upora, lahko izračunamo maksimalni padec napetosti oziroma maksimalno napetost na uporu.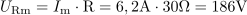

Efektivna vrednost napetosti na uporu oziroma padec napetosti na uporu je: U_R =
132
V.
Pri znani maksimalni napetosti na ohmskem uporu lahko po deljenju z ustreznim faktorjem glede na obliko napetosti pridemo do efektivne vrednosti napetosti.

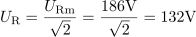Skozi tokokrog teče efektivni tok: I =
4.4
A.
Za izračun efektivne napetosti na tuljavi potrebujemo efektivni tok, ki teče skozi tuljavo oziroma skozi induktivno upornost tuljave.

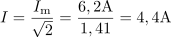Pri frekvenci 50 Hz ima tuljava induktivno upornost: X_L =
40
Ω.
Induktivno upornost tuljave lahko določimo, ker poznamo induktivnost tuljave in frekvenco napetosti oziroma toka.

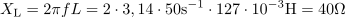Vrednost efektivne napetosti na tuljavi je: U_L =
176
V.
Pri znanem efektivnem toku skozi tuljavo in znani induktivni upornosti tuljave določimo padec napetosti na tuljavi.

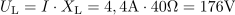Generator daje efektivno napetost: U =
220
V.
Efektivno napetost na uporu in na tuljavi, ki pa nista v fazi, poznamo, zato lahko izračunamo napetost, ki jo daje generator za pokrivanje teh padcev napetosti. Za izračun geometrične vsote napetosti uporabimo Pitagorov izrek.

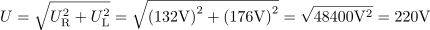Navidezna moč generatorja je: S =
968
VA.
Navidezno moč generatorja določa produkt toka in napetosti.

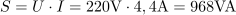Kosinus faznega kota φ med tokom in napetostjo v zaporedni RL vezavi je: cosφ =
0.6
.
Delovno moč lahko izračunamo iz navidezne moči generatorja z upoštevanjem kosinusa faznega kota φ med tokom in napetostjo generatorja. Tega lahko dobimo npr. iz razmerja med napetostjo na ohmski upornosti in celotno napetostjo.

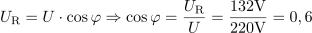Za napajanje zaporedne vezave ohmske upornosti in tuljave oddaja generator delovno moč: P =
581
W.
Ker poznamo kosinus faznega kota med tokom in napetstjo, lahko izračunamo delovno moč iz navidezne moči, saj sta ti dve moči tudi v razmerju kosinusa faznega kota φ.

1. odgovor
2.
3.
4.
5.
6.
7.
8.
9.
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Namig

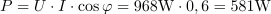dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 18

0

Rešeni primer 18
Zaporedno vezana upor z upornostjo 20 Ω in tuljava z induktivnostjo 10 mH sta priključena na napetost 140 V frekvence 500 Hz. Izračunaj tok, padca napetosti na obeh elementih in fazni kot med napetostjo in tokom.
7
Tuljava ima pri frekvenci 500 Hz induktivno upornost: X_L =
31.4
Ω.
Upornost ohmskega upora je že podana, izračunati pa moramo induktivno upornost tuljave.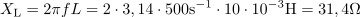

Zaporedna vezava ohmskega upora in tuljave ima impedanco: Z =
37.2
Ω.
Na tok v vezju vpliva impedanca vezja, ki jo določata ohmska in induktivna upornost, zato jo izračunamo.

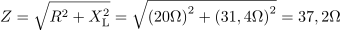Skozi vezje teče tok: I =
3.8
A.
Tok v vezju je po Ohmovem zakonu odvisen od napetosti in impedance vezja.

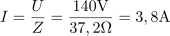Padec napetosti na uporu znaša: U_R =
75
V.
Tok povzroča na uporu padec napetosti, ki je odvisen od njegove upornosti.

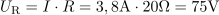Padec napetosti na tuljavi je pri toku 3,8 A: U_L =
0
Tok, ki teče skozi vezje, povzroča padec napetosti tudi na tuljavi in je odvisen od njene induktivne upornosti.

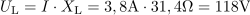Skupen padec napetosti na ohmskem uporu in na tuljavi je: U =
140
V.
Z izračunom geometrične vsote napetosti U_R in U_L lahko preverimo, če je skupen padec napetosti res enak napetosti generatorja.

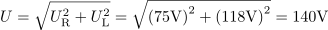Med tokom skozi vezje in napetostjo generatorja je fazni kot: φ =
57
°.
Fazni kot φ med tokom in napetostjo lahko izračunamo po več poteh: iz razmerja med ohmsko in celotno upornostjo, razmerja med induktivno in ohmsko upornostjo, razmerja med padcem napetosti na tuljavi in celotno napetostjo, razmerja med padcem napetosti na tuljavi in padcem napetosti na uporu, itd.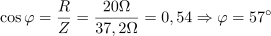

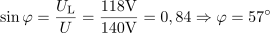1. odgovor
2.
3.
4.
5.
6.
7.
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Namig

dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 19

0

Rešeni primer 19
Tuljavo z ohmsko upornostjo R in induktivnostjo L priključimo zaporedno na enosmerno napetost 6,2 V in pri tem teče skoznjo tok 0,75 A. Ko pa tuljavo priključimo na sinusno izmenično napetost 100 V frekvence 50 Hz, je tok skozi tuljavo 0,8 A. Kolikšna je induktivnost tuljave?
4
Ohmska upornost tuljave je: R =
8.3
Ω.
Ker ima realna tuljava poleg induktivne upornosti tudi ohmsko upornost, jo obravnavamo kot zaporedno RL vezavo. Ko tuljavo vključimo v enosmerni tokokrog, tuljava nima induktivne upornosti oziroma je 0 Ω, zato enostavno izračunamo njeno ohmsko upornost.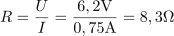

Pri frekvenci generatorja 50 Hz je impedanca tuljave: Z =
125
Ω.
V izmeničnem tokokrogu vplivata na tok skozi tuljavo tako njena ohmska kot induktivna upornost, zato iz napetosti in toka skozi tuljavo lahko izračunamo impedanco tuljave.

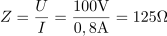Tuljava ima pri frekvenci 50 Hz poleg ohmske upornosti 8,3 Ω tudi induktivno upornost: X_L =
124.7
Ω.
Ko poznamo ohmsko upornost tuljave in njeno impedanco pri določeni frekvenci, lahko pri nespremenjenih razmerah izračunamo induktivno upornost tuljave.

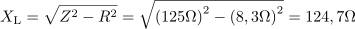Tuljava v tokokrogu ima induktivnost: L =
0.4
H.
Sedaj, ko poznamo induktivno upornost tuljave pri frekvenci 50 Hz, lahko enostavno izračunamo induktivnost tuljave.

1. odgovor
2.
3.
4.
0
0
0
0
0
0
0
0

Namig

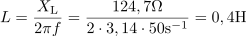dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 20

0

Rešeni primer 20
Izračunaj fazni kot med napetostjo in tokom za zaporedno vezavo ohmskega upora z upornostjo 800 Ω in kondenzatorja s kapacitivnostjo 0,1 μF pri frekvenci 2 kHz.
2
Kapacitivna upornost kondenzatorja pri frekvenci 2000 Hz je: X_C =
796
Ω.
Ker že poznamo ohmsko upornost vezave, izračunamo še kapacitivno upornost v podanih razmerah in v naslednjem koraku lahko že izračunamo fazni kot.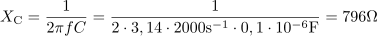

Fazni kot med napetostjo in tokom je: φ =
-45
°.
Iz razmerja kapacitivne in ohmske upornosti lahko izračunamo tangens faznega kota in posledično tudi fazni kot. Upoštevamo, da napetost zaostaja za tokom.

1. odgovor
2.
0
0
0
0

Namig

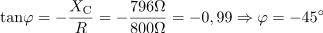dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 21

0

Rešeni primer 21
Izračunaj tok skozi zaporedno vezavo upora 10 Ω in kondenzatorja s kapacitivnostjo 300 μF pri frekvenci 50 Hz, če je vezava priključena na napetost 10 V.
3
Kapacitivna upornost kondenzatorja pri podani frekvenci znaša: X_C =
10.6
Ω.
Impedanco vezja lahko izračunamo, če poznamo ohmsko in kapacitivno upornost, zato poiščemo še kapacitivno upornost.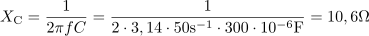

Impedanca zaporedne vezave upora in kondenzarja je: Z =
14.5
Ω.
Za izračun impedance vezja uporabimo Pitagorov izrek, s katerim združimo ohmsko upornost in kapacitivno upornost.

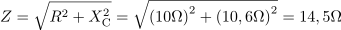Pri frekvenci 50 Hz teče skozi zaporedno vezavo upora in kondenzatorja tok: I =
0.69
A.
Tok skozi vezje določa napetost generatorja in impedanca vezja.

1. odgovor
2.
3.
0
0
0
0
0
0

Namig

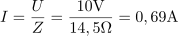dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 22

0

Rešeni primer 22
Upor z upornostjo 30 Ω in kondenzator s kapacitivnostjo 220 μF sta vezana zaporedno in priključena na izmenično napetost 220 V frekvence 50 Hz. Izračunaj efektivno vrednost toka, napetosti na uporu in kondenzatorju, fazni kot ter vse moči.
10
Kondenzator s kapacitivnostjo 220 μF ima pri frekvenci 50 Hz kapacitivno upornost: X_C =
14.5
Ω.
Za izračun kapacitivne upornosti upoštevamo frekvenco napetosti in kapacitivnost kondenzatorja.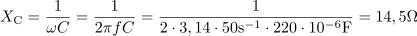

RC vezje ima impedanco: Z =
33.3
Ω.
Ker že poznamo ohmsko upornost R in kapacitivno upornost XC, lahko takoj izračunamo impedanco vezja Z.

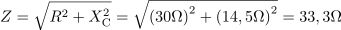Skozi vezje teče tok z efektivno vrednostjo: I =
6.61
A.
Efektivno vrednost toka izračunamo po Ohmovem zakonu iz priključene napetosti in impedance vezja.

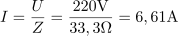Padec napetosti na ohmskem uporu znaša: U_R =
198.2
V.
Tok, ki teče skozi vezje, povzroča na ohmskem uporu padec napetosti. Efektivna napetost na uporu je odvisna od efektivnega toka in upornosti upora.

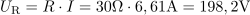Padec napetosti na kondenzatorju znaša: U_C =
95.8
V.
Tok, ki teče skozi vezje, povzroča padec napetosti tudi na kondenzatorju, in je odvisen od efektivnega toka in vrednosti kapacitivne upornosti.

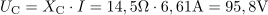V zaporednem izmeničnem krogu z RC bremenom napetost zaostaja za tokom za fazni kot: φ =
-25.8
°.
Fazni kot lahko izračunamo na različne načine. Eden od načinov omogoča izračun preko tangensa faznega kota, ki je določen z razmerjem kapacitivne in ohmske upornosti.

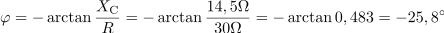Generator daje navidezno moč: S =
1454
VA.
Navidezno moč generatorja določa zmnožek efektivnega toka in efektivne napetosti v vezju.

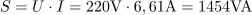V vezju se sprošča delovna moč: P =
1310
W.
Delovna moč se sprošča na ohmski upornosti vezja, zato jo ob znanih podatkih lahko izračunamo.

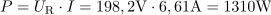Kapacitivna jalova moč v vezju je: Q_C =
633
var.
Tok, ki teče skozi kondenzator, povzroča prenos jalove moči, zato jo izračunamo iz produkta efektivnega toka in padca napetosti na kondenzatorju.

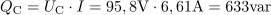Navidezna moč generatorja je: S =
1454
VA.
S preizkusom se prepričamo, če je navidezna moč res enaka geometrični vsoti delovne moči in kapacitivne jalove moči.

1. odgovor
2.
3.
4.
5.
6.
7.
8.
9.
10.
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Namig

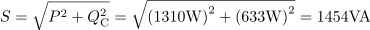dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 23

0

Rešeni primer 23
Zaporedna vezava upora in kondenzatorja je priključena na izmenično napetost 120 V frekvence 50 Hz. Skozi vezje teče tok 2 A. Delovna moč je 144 W. Izračunaj ohmsko upornost upora in kapacitivnost kondenzatorja.
5
Upor v vezju ima ohmsko upornost: R =
36
Ω.
Iz podane delovne moči in toka skozi vezje lahko izračunamo ohmsko upornost upora.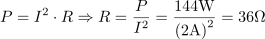

Navidezna moč za podano vezje je: S =
240
VA.
Ker sta podana tok in napetost, lahko izračunamo navidezno moč, preko nje pa jalovo moč in končno tudi kapacitivno upornost kondenzatorja.

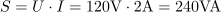Jalova moč vezja je: Q_C =
192
var.
Ker vemo, da je navidezna moč geometrična vsota delovne in jalove moči, lahko pri znani navidezni in delovni moči izračunamo jalovo moč.

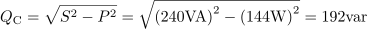Vezje ima kapacitivno upornost: X_C =
48
Ω.
Iz navidezne moči, ki smo jo pravkar določili, in efektivnega toka skozi vezje, izračunamo kapacitivno upornost vezja oziroma kondenzatorja.

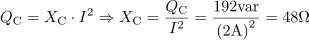Kondenzator v vezju ima kapacitivnost: C =
66.3
μF.
Pri znani kapacitivni upornosti je izračun kapacitivnosti kondenzatorja enostaven, saj je kapacitivna upornost odvisna od kapacitivnosti in frekvence.

1. odgovor
2.
3.
4.
5.
0
0
0
0
0
0
0
0
0
0

Namig

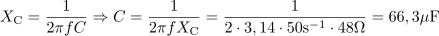dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 24

0

Rešeni primer 24
Na napetost 220 V frekvence 50 Hz je priključena zaporedna vezava upora z upornostjo 50 Ω, tuljave z induktivnostjo 40 mH in kondenzatorja s kapacitivnostjo 50 μF. Izračunaj efektivno vrednost toka in napetosti na posameznih elementih ter vse moči, faktor moči in fazni kot.
14
Tuljava ima pri frekvenci 50 Hz induktivno upornost: X_L =
12.56
Ω.
Na razpolago imamo vse podatke za izračun induktivne in kapacitivne upornosti, to je frekvenco, kapacitivnost in induktivnost.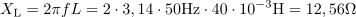

Kondenzator ima pri frekvenci 50 Hz kapacitivno upornost: X_C =
63.7
Ω.
Tako kot smo izračunali induktivno upornost, določimo še kapacitivno upornost.

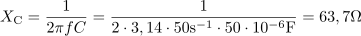Impedanca vezave z zaporedno vezanimi elementi RLC je: Z =
71.5
Ω.
Ker poznamo vse upornosti v tokokrogu, lahko izračunamo impedanco vezave.

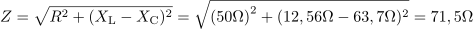V vezavi teče efektivni tok: I =
3.1
A.
Napetost generatorja in impedanca vezave določata efektivni tok v tokokrogu.

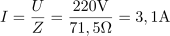Tok povzroča na uporu padec napetosti: U_R =
155
V.
Efektivni tok in upornosti posameznih elementov določajo padce napetosti na elementih. Najprej izračunamo padec napetosti na uporu.

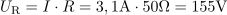Na tuljavi se pojavi padec napetosti: U_L =
38.9
V.
Tudi na tuljavi je po Ohmovem zakonu padec napetosti določen z njeno induktivno upornostjo in s tokom skoznjo.

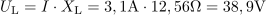Padec napetosti na kondenzatorju je: U_C =
197.5
V.
Na kondenzatorju povzroča padec napetosti tok skozi kapacitivno upornost kondenzatorja.

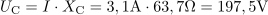Navidezna moč za podano RLC vezje je: S =
682
VA.
Navidezno moč generatorja izračunamo iz efektivne napetosti in efektivnega toka.

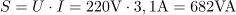V vezju se troši delovna moč: P =
480.5
W.
Delovna moč se troši na uporu R, ko skozenj teče efektivni tok I.

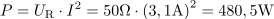Jalova moč ima kapacitivni značaj in znaša: Q =
491.4
var.
Jalova moč v vezju predstavlja moč na jalovih komponentah, to je na tuljavi in kondenzatorju. Del moči na teh komponentah se kompenzira, zato jalova moč zajema le razliko jalove moči med njima.

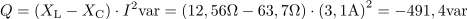Velikost induktivne jalove moči na tuljavi je: Q_L =
120.4
var.
Induktivna jalova moč na tuljavi je odvisna od induktivne upornosti tuljave in toka skozi tuljavo.

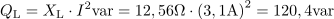Velikost induktivne jalove moči na tuljavi je: Q_C =
612.2
var.
Kapacitivna jalova moč na kondenzatorju je odvisna od kapacitivne upornosti kondenzatorja in toka skozi kondenzator.

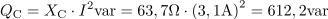Faktor moči za podano vezavo je: cosφ =
0.7
.
Faktor moči dobimo iz razmerja med delovno in navidezno močjo vezave, lahko pa ga izračunamo tudi iz razmerja med ohmsko upornostjo in impedanco vezave ali pa iz razmerja med padcem napetosti na uporu in napetostjo generatorja.

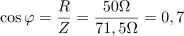Zaradi prevladujočega značaja kapacitivnega bremena je fazni kot: φ =
-45.6
°.
Za določitev faznega kota φ je pomemben tudi predznak, ki ga določa značaj vezja, to je razlika med induktivno in kapacitivno upornostjo. Če prevlada induktivna obremenitev, je predznak pozitiven, pri kapacitivni pa negativen. Fazni kot lahko izračunamo tudi preko tangensa faznega kota, ki je določen z razmerjem med jalovimi komponentami upornosti in celotno impedanco vezave.

1. odgovor
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Namig

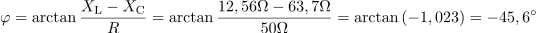dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 25

0

Rešeni primer 25
Dva kondenzatorja, dve tuljavi in upor so vezani zaporedno. Kapacitivnost prvega kondenzatorja je 1,6 μF, drugega pa 0,4 μF, induktivnost prve tuljave je 69 mH, druge pa 0,11 H. Ohmsko upornost prve tuljave zanemarimo, pri drugi pa je njena upornost 100 Ω. Upornost upora je 500 Ω. Vezava je priključena na napetost 100 V frekvence 400 Hz. Izračunaj tok in navidezno moč.
10
Vezje ima ohmsko upornos: R =
600
Ω.
Za izračun toka potrebujemo impedanco vezja. Pri računanju impedance neposredno ločeno seštejemo vse induktivne, vse kapacitivne in vse ohmske upornosti, nato pa izračunamo geometrično vsoto vseh treh tipov upornosti.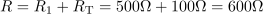

Induktivna upornost prve tuljave je: X_L1 =
173.4
Ω.
Podobno kot smo postopali z ohmskimi upornostmi, združimo tudi vse induktivne upornosti, ki pa jih najprej določimo za posamezne tuljave.

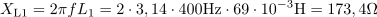Druga tuljava ima induktivno upornost: X_L2 =
276.3
Ω.
Tudi za drugo tuljavo izračunamo njeno induktivno upornost pri frekvenci 400 Hz.

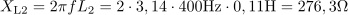Skupna induktivna upornost vezave je: X_L =
449.7
Ω.
V naslednjem koraku združimo induktivni upornosti obeh tuljav.

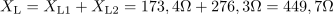Prvi kondenzator ima kapacitivno upornost: X_C1 =
248.8
Ω.
Na enak način kot smo izračunali posamezne induktivne upornosti in jih nato združili, postopamo tudi s kapacitivnimi upornostmi.

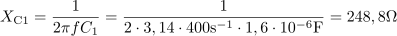Kapacitivna upornost drugega kondenzatorja je: X_C2 =
995.2
Ω.
Na enak način določimo tudi kapacitivno upornost drugega kondenzatorja.

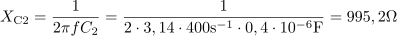Kapacitivna upornost celotne vezave je: X_C =
1244
Ω.
Tudi kapacitivni upornosti obeh kondenzatorjev združimo v skupno kapacitivno upornost.

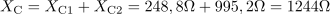Vezje ima impedanco: Z =
995.4
Ω.
Izračunamo impedanco celotnega vezja z zaporedno vezanimi elementi R, L in C.

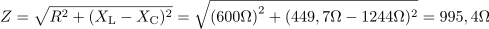Skozi vezje teče efektivni tok: I =
0.1
A.
Efektivni tok izračunamo po Ohmovem zakonu, saj ga določa pritisnjena napetost in impedanca vezja.

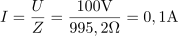Navidezna moč zaporedne vezave dveh tuljav, dveh kondenzatorjev in upora znaša: S =
10
VA.
Za izračun navidezne moči potrebujemo napajalno napetost in tok skozi vezje.

1. odgovor
2.
3.
4.
5.
6.
7.
8.
9.
10.
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Namig

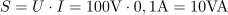dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 26

0

Rešeni primer 26
Vzporedna vezava upora z upornostjo 5 Ω in tuljave z induktivnostjo 3 mH je priključena na izmenično napetost 7 V frekvence 160 Hz. Izračunaj vse tokove v vezju in admitanco vezja.
5
V veji z ohmskim uporom teče tok: I_R =
1.4
A.
Vsak od elementov v vzporedni vezavi je priključen neposredno na napetost izvora napetosti, zato lahko izračunamo tokove skozi posamezne veje neposredno po Ohmovem zakonu.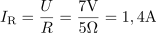

Tuljava ima induktivno upornost: X_L =
3
Ω.
Za izračun toka skozi tuljavo moramo poznati induktivno upornost tuljave.

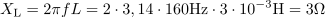V veji s tuljavo teče tok: I_L=
2.33
A.
Tok skozi tuljavo določa napetost generatorja in induktivna upornost tuljave.

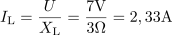Iz generatorja teče v vezje tok: I =
2.72
A.
Skupni tok skozi vezje izračunamo z geometrično vsoto toka skozi upor in toka skozi tuljavo. Uporabimo Pitagorov izrek.

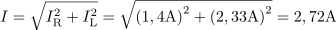Vzporedno RL vezje ima admitanco: Y =
0.39
S.
Admitanco vezja izračunamo kot geometrično vsoto ohmske in induktivne prevodnosti v vezavi.

1. odgovor
2.
3.
4.
5.
0
0
0
0
0
0
0
0
0
0

Namig

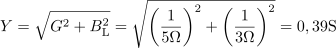dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 27

0

Rešeni primer 27
V vzporedni vezavi upora z upornostjo 500 Ω in tuljave, katere induktivnosti ne poznamo, je fazni kot med napetostjo in tokom 45 °. Kolikšno upornost R_X moramo še vezati vzporedno, da se bo fazni kot zmanjšal za 10 °?
4
Prevodnost ohmskega upora je: G =
0.002
S.
V vzporedni vezavi elementov računamo s prevodnostmi. Za boljšo ponazoritev problema si pomagamo s kazalčnim diagramom. Pred spremembo je fazni kot φ, po spremembi, ki jo povzroči dodan upor R_X pa φ₁. Pred spremembo je prevodnost ohmskega upora G, po spremembi z dodanim uporom R_X pa G₁. Prevodnost induktivne veje se ne spremeni in ostaja enaka B_L. Primerjavo izvedemo na osnovi tangensov faznih kotov φ in φ₁, ki sta določena z razmerji med induktivno in ohmsko prevodnostjo.
V prvem koraku izračunamo prevodnost ohmskega upora in prevodnost induktivne veje s tuljavo B_L.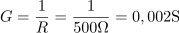

Induktivna veja v vezju ima prevodnost: B_L =
0.002
S.
Prevodnost induktivne veje lahko izračunamo iz razmerja med induktivno prevodnostjo in prevodnostjo ohmskega upora, ki določa fazni kot φ.

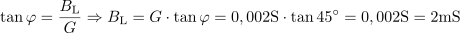Dodatni upor, ki fazni kot zmanjša za 10 º, ima prevodnost: G_X =
0.8
mS.
Tudi pri iskanju dodatnega neznanega upora oziroma prevodnosti si pomagamo z enačbo za tangens faznega kota. Ker že poznamo prevodnost tuljave, prevodnost prvotnega upora in želen fazni kot φ₁, je mogoče s temi podatki izračunati prevodnost dodatnega neznanega upora.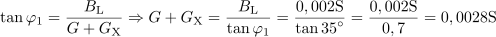

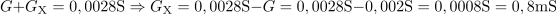Dodatni upor, ki fazni kot zmanjša za 10 º, ima upornost: R_X =
1250
Ω.
Sedaj, ko poznamo prevodnost dodatnega upora G_X, izračunamo še njegovo upornost R_X.

1. odgovor
2.
3.
4.
0
0
0
0
0
0
0
0

Namig

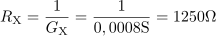dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 28

0

Rešeni primer 28
Kondenzator s kapacitivnostjo 10 μF in upor z neznano upornostjo sta vezana vzporedno in priključena na napetost 12 V frekvence 100 Hz. Impedanca vezave je 100 Ω. Izračunaj ohmsko upornost, tok v vezje in vse moči.
8
Kondenzator ima kapacitivno prevodnost: B_C =
0.0063
S.
Ker v vzporednih vezavah računamo s prevodnostmi, izračunamo v prvem koraku kapacitivno prevodnost kondenzatorja.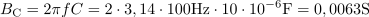

Admitanca vzporedne vezave upora in kondenzatorja je: Y =
0.01
S.
Ker poznamo impedanco vezave in računamo s prevodnostmi, bomo določili tudi admitanco vezave.

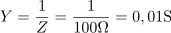Ohmski upor ima prevodnost: G =
7.8
mS.
Iz admitance vezja in kapacitivne prevodnosti kondenzatorja izračunamo prevodnost ohmskega upora.

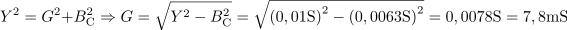Upor, ki je priključen vzporedno kondenzatorju, ima upornost: R =
128.2
Ω.
Pri znani prevodnosti ohmskega upora določimo še njegovo upornost.

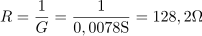V vezje teče tok: I =
120
mA.
Napetost, na katero je priključeno vezje, poznamo, prav tako upornost vezja, zato lahko izračunamo tok v vezje.

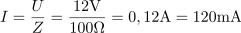Navidezna moč vezja je: S =
1.44
VA.
Tok in napetost določata navidezno moč.

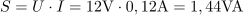Delovna moč v vezju znaša: P =
1.12
W.
Delovna moč se sprošča na ohmskem uporu. Za njen izračun poznamo napetost in upornost upora.

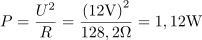Navidezna moč v vezju je: Q_C =
0.91
var.
Izračunati moramo še navidezno moč vezja, za katero imamo tudi vse podatke, to je napetost in kapacitivno prevodnost kondenzatorja.

1. odgovor
2.
3.
4.
5.
6.
7.
8.
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Namig

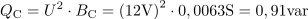dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 29

0

Rešeni primer 29
Admitanca vzporedne RC vezave je 0,2 S, fazni kot pa -30 °. Izračunaj ohmsko upornost in delovno moč, če je navidezna moč 20 VA.
3
Ohmski upora ima prevodnost: G =
0.173
S.
Kosinus faznega kota, prevodnost ohmskega upora in admitanco vezja med seboj povežemo z ustrezno enačbo in dobimo podatek o omskem uporu.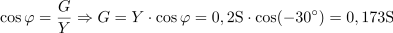

Ohmski upor ima upornost: R =
5.78
Ω.
V naslednjem koraku poiščemo upornost upora na osnovi njegove prevodnosti.

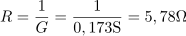Delovna moč, ki se sprošča v RC vezju, je: P =
17.3
W.
Fazni kot med drugim tudi povezuje navidezno in delovno moč. Poznamo fazni kot oziroma faktor moči in navidezno moč, iščemo pa delovno moč.

1. odgovor
2.
3.
0
0
0
0
0
0

Namig

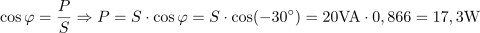dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 30

0

Rešeni primer 30
Sinusna napetost 120 V napaja vzporedno vezavo, ki jo predstavljajo upor, tuljava in kondenzator. Tokovi, ki jih požene napetost po posameznih vejah, imajo naslednje vrednosti: 3 A skozi upor, 6 A skozi tuljavo in 2 A skozi kondenzator. Določi upornosti in prevodnosti posameznih elementov ter admitanco vezave.
7
Upornost ohmskega upora v vzporedni RLC vezavi je: R =
40
Ω.
Tok v vsaki veji določa Ohmov zakon, ki povezuje napajalno napetost, upornost v veji in tok. Na tej osnovi tudi izračunamo upornosti elementov v posameznih vejah, pa tudi pripadajoče prevodnosti.
V prvem koraku poiščemo upornost in prevodnost upora.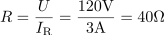

Prevodnost tega tega upora pa je: G =
25
mS.
Tok v vsaki veji določa Ohmov zakon, ki povezuje napajalno napetost, upornost v veji in tok. Na tej osnovi tudi izračunamo upornosti elementov v posameznih vejah, pa tudi pripadajoče prevodnosti.
V prvem koraku poiščemo upornost in prevodnost upora.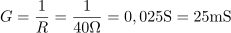

Induktivna upornost tuljave je: X_L =
20
Ω.
Tako kot smo izračunali upornost in prevodnost upora, določimo ta dva parametra tudi za tuljavo, saj poznamo efektivni tok skozi tuljavo pri znani napajalni napetosti.

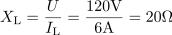Tuljava ima induktivno prevodnost: B_L =
50
mS.
Tako kot smo izračunali upornost in prevodnost upora, določimo ta dva parametra tudi za tuljavo, saj poznamo efektivni tok skozi tuljavo pri znani napajalni napetosti.

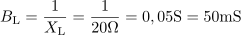Kondenzator ima kapacitivno upornost: X_C =
60
Ω.
Postopek za izračun upornosti in prevodnosti kondenzatorja je enak postopku za izračun upornosti in prevodnosti tuljave.

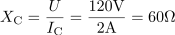Kapacitivna prevodnost kondenzatorja pa je: B_C =
16.7
mS.
Postopek za izračun upornosti in prevodnosti kondenzatorja je enak postopku za izračun upornosti in prevodnosti tuljave.

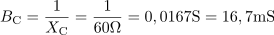Admitanca vezja z vzporedno vezanimi elementi RLC znaša: Y =
41.6
mS.
Admitanco vezja izračunamo kot geometrično vsoto prevodnosti posameznih elementov vezja.

1. odgovor
2.
3.
4.
5.
6.
7.
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Namig

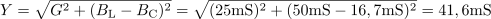dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 31

0

Rešeni primer 31
Vzporedno vezani elementi upor, tuljava in kondenzator so priključeni na napetost 40 V frekvence 200 Hz. Delovna moč je 40 W, induktivna jalova moč pa 20 var. Izračunaj upornost upora, induktivnost tuljave in kapacitivnost kondenzatorja, če je fazni kot -45 °.
5
Upornost upora, na katerem se sprošča delovna moč, je: R =
40
Ω.
Izhajamo iz znane delovne moči in napetosti, kar nam omogoča izračun ohmske upornosti upora.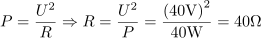

Induktivna upornost tuljave je: X_L =
80
Ω.
Tudi za izračun induktivne upornosti je pristop enak, saj poznamo induktivno jalovo moč in napetost. Na tej osnovi izračunamo induktivno upornost.

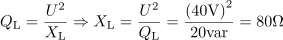Tuljava, ki ima pri 200 Hz induktivno upornost 80 Ω, ima induktivnost: L =
64
mH.
Ko poznamo induktivno upornost tuljave, je le še en korak do induktivnosti, saj poznamo tudi frekvenco, pri kateri ima tuljava tolikšno upornost.

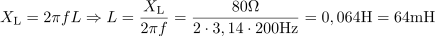Kapacitivna prevodnost v vezju znaša: B_C =
37.5
mS.
Do kapacitivnosti kondenzatorja pridemo posredno, z izračunom kapacitivne prevodnosti B_C ali pa tudi preko izračuna kapacitivne jalove moči Q_C.
Tangens faznega kota povezuje jalovo prevodnost (B_L – B_C) in delovno prevodnost G, zato iz te povezave lahko izračunamo kapacitivno prevodnost B_C.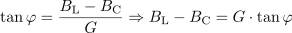

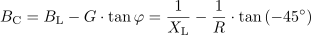
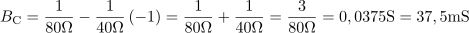Kondenzator v vzporedni RLC vezavi ima kapacitivnost: C =
29.9
μF.
Iz kapactivne prevodnosti pa pri znani frekvenci 200 Hz enostavno določimo kapacitivnost.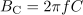

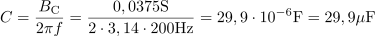1. odgovor
2.
3.
4.
5.
0
0
0
0
0
0
0
0
0
0

Namig

dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 32

0

Rešeni primer 32
Z uporabo kompleksnega računa izračunaj impedanco in vse tokove danega vezja. Vezje določajo naslednji podatki: R1 = 80 Ω, R2 = 260 Ω, L = 0,19 H, C = 21,2 μF, U = 120 V, f = 50 Hz.
9
Induktivna upornost v veji z uporom R₁ je: X_L =
60
Ω.
Impedanca veje z uporom R₁ je: Z₁ = 100 Ω.
Fazni kot v veji z uporom R₁ je: φ₁ = 37 º.
Zanima nas impedanca vezja. Pred uporabo kompleksorjev za izračun impedance, izračunamo induktivno in kapacitivno upornost, impedanco vsake veje in fazni kot za vsako vejo.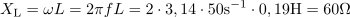

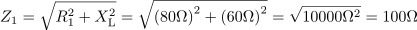
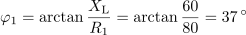Kapacitivna upornost v veji z uporom R₂ je: X_C =
150
Ω.
Impedanca veje z uporom R₂ je: Z₂ = 300 Ω.
V veji z uporom R₂ je fazni kot: φ₂ = 30 º.
Na enak način pripravimo podatke še za drugo vejo.

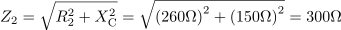
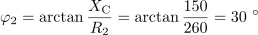Impedanco v veji z uporom R₁ lahko zapišemo s kompleksorjem v komponentni obliki kot: Z₁ =
0
Ω.
Isto impedanco lahko zapišemo s kompleksorjem tudi v eksponentni obliki kot: Z₁ = 100 ∙ e^j37º Ω.
Na osnovi dobljenih podatkov najprej zapišemo kompleksor impedance Z₁ za vejo z uporom R₁.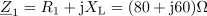

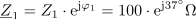Impedanco v veji z uporom R₂ zapišemo s kompleksorjem v komponentni obliki kot: Z₂ =
0
Ω.
Zapis impedance Z₂ s kompleksorjem v eksponentni obliki pa ima obliko: Z₂ = 300 ∙ e^-j30º Ω.
Tudi za vejo z uporom R₂ izvedemo zapis impedance v obliki kompleksorja.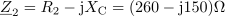

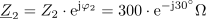Impedanca vezja zapisana s kompleksorjem v eksponentni obliki je: Z =
86
∙ e^j22º Ω.
Celotno impedanco vezave lahko enostavno izračunamo tako, da združimo vzporedno vezani impedanci Z₁ in Z₂ .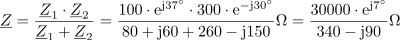

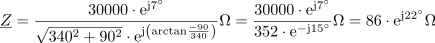Celoten tok v vezje zapišemo s kompleksorjem v eksponentni obliki: I =
1.4
∙ e^-j22º A.
Zapis celotnega toka v vezje s kompleksorjem po komponentah pa ima obliko: I = (1,31-j0,52) A.
Tok izračunamo po Ohmovem zakonu, vendar tudi pri tem računanju uporabljamo kompleksorje.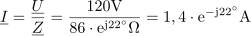

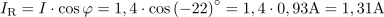
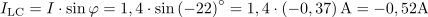
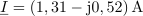V veji z uporom R₁ zapišemo tok s kompleksorjem v eksponentni obliki: I₁ =
1.2
∙ e^-j37º A.
Isti tok lahko zapišemo s kompleksorjem tudi v komponentni obliki: I₁ = (0,96 ^–j0,72) A.
Tudi do izračuna tokov I₁ in I₂ vodi pot preko uporabe Ohmovega zakona.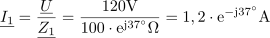

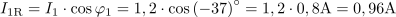
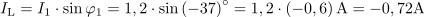
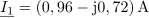Tok, ki teče v veji z uporom R₂, zapišemo s kompleksorjem v eksponentni obliki: I₂ =
0.4
∙ e^j30º A.
Ta tok pa lahko zapišemo s kompleksorjem tudi po komponentah v obliki: I₂ = (0,35 + j0,20) A.
Na enak način kot smo izračunali tok v veji z uporom R₁, opravimo izračun toka še v drugi veji z uporom R₂.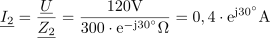

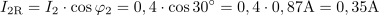
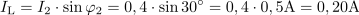
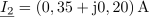Preizkus pravilnosti izračuna je pokazal, da je pri tokih I₁ = (0,96–j0,72) A in I₂ = (0,35+j0,20) A, skupni tok v vezje: I =
0
A.
V zadnjem koraku izvedemo še preizkus pravilnosti izračuna tokov, v katerem primerjamo skupni tok I, s tokovoma I₁ in I₂. Preizkus opravimo z uporabo Kirchhoffovega zakona.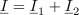

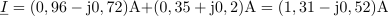1. odgovor
2.
3.
4.
5.
6.
7.
8.
9.
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Namig

dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 33

0

Rešeni primer 33
Za narisano vezavo izračunaj upornost upora R_X tako, da bo fazni kot med napetostjo in tokom 22 °. Znane so upornosti ostalih komponent R = 20 Ω, X_L = 60 Ω in X_C = 80 Ω.
2
Impedanca vezja, vključno z neznano upornostjo R_X, je: Z =
0
Ω.
Pri določanju neznane upornosti bomo izhajali iz tangensa faznega kota φ, ki ga poznamo in je določen z razmerjem med imaginarno in realno komponento impedance vezja:

. V prvem koraku združimo vse komponente v skupni kompleksor impedance vezja Z.

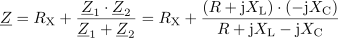
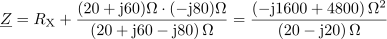
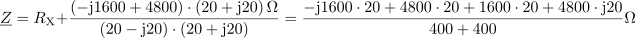
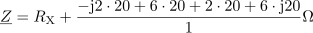
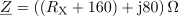Neznani upor ima ohmsko upornost: R_X =
40
Ω.
S pomočjo enačbe za tangens faznega kota

lahko iz enačbe izrazimo neznano upornost R_X in ji določimo vrednost.

1. odgovor
2.
0
0
0
0

Namig

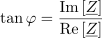
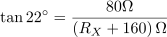
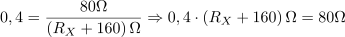
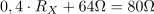
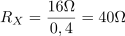dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 34

0

Rešeni primer 34
Upor z upornostjo 44 Ω, tuljava z induktivnostjo 0,64 H in kondenzator s kapacitivnostjo 15,9 μF so vezani zaporedno in priključeni na napetost 220 V. Izračunaj resonančno frekvenco. Kolikšen je tedaj tok in kolikšne so vrednosti posameznih napetosti?
8
Resonančna frekvenca zaporednega RLC nihajnega kroga je: f_r =
50
Hz.
Izračunamo resonančno frekvenco, pri kateri je induktivna upornost enaka kapacitivni upornosti.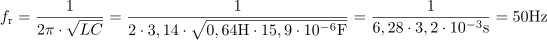

Impedanca nihajnega kroga znaša pri resonančni frekvenci 50 Hz: Z =
44
Ω.
Ker se pri resonančni frekvenci induktivna in kapacitivna upornost med seboj odštejeta, ima impedanca, ki vpliva na tok, čisto ohmski značaj.

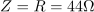Pri resonačni frekvenci ima tok skozi vezje velikost: I_r =
5
A.
Resonančni tok določata napajalna napetost in impedanca vezja.

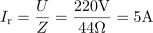Induktivna upornost tuljave pri resonančni frekvenci je: X_Lr =
200
Ω.
Za izračun napetosti na tuljavi pri resonančni frekvenci potrebujemo induktivno upornost tuljave, zato jo izračunamo.

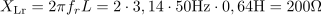Padec napetosti na tuljavi je pri resonančni frekvenci: U_Lr =
1000
V.
Padec napetosti na tuljavi izračunamo po Ohmovem zakonu preko toka in induktivne upornosti.

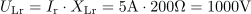Kapacitivna upornost kondenzatorja je pri resonančni frekvenci: X_Cr =
200
Ω.
Za izračun napetosti na kondenzatorju potrebujemo kapacitivno upornost kondenzatorja.

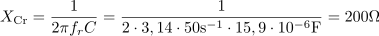Pri resonančni frekvenci znaša padec napetosti na kondenzatorju: U_Cr =
1000
V.
Padec napetosti na kondenzatorju izračunamo po Ohmovem zakonu preko toka in kapacitivne upornosti.

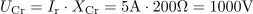Padec napetosti na uporu je: U_r =
220
V.
Ker gre za resonanco, je padec napetosti na uporu kar enak napetosti izvora.

1. odgovor
2.
3.
4.
5.
6.
7.
8.
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Namig

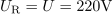dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 35

0

Rešeni primer 35
Zaporedno RLC vezje je pri frekvenci 800 Hz v resonanci. Tedaj je napetost na kondenzatorju 2 V. Resonančni tok znaša 1 mA, na uporu pa se sprošča moč 10 μW. Izračunaj ohmsko upornost, induktivnost, kapacitivnost in valovno impedanco ter kvaliteto nihajnega kroga.
8
Upornost ohmskega upora je: R =
10
Ω.
Na osnovi podane moči in toka skozi upor imamo dostop do upornosti upora.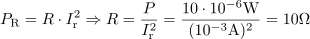

Napetost izvora je enaka napetosti na uporu in znaša: U =
10
mV.
Ker je nihajni krog v resonanci, je napetost na uporu enaka napetosti izvora.

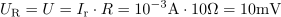Kvaliteta nihajnega kroga je: Q =
200
.
Ker poznamo napetost izvora in napetost na kondenzatorju, ki je enaka tudi napetosti na tuljavi, lahko izračunamo kvaliteto nihajnega kroga.

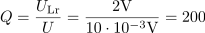Tuljava v zaporednem nihajnem krogu ima pri resonančni frekvenci induktivno upornost: X_Lr =
2000
Ω.
Ker je kvaliteta pri zaporednem RLC krogu določena tudi z razmerjem med induktivno in ohmsko upornostjo nihajnega kroga, lahko že izračunamo induktivno upornost tuljave v nihajnem krogu.

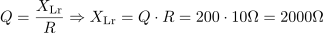Tuljava v nihajnem krogu ima induktivnost: L =
0.4
H.
Ker poznamo induktivno upornost in resonančno frekvenco, lahko določimo induktivnost tuljave.

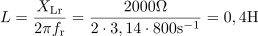Kondenzator ima pri resonančni frekvenci kapacitivno upornost: X_Cr =
2000
Ω.
Pri pogojih resonance je v zaporednem nihajnem krogu napetost na tuljavi enaka napetosti na kondenzatorju, zato je tudi kapacitivna upornost enaka induktivni upornosti.

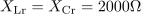Kapacitivnost kondenzatorja v nihajnem krogu je: C =
0.1
μF.
Pri znani kapacitivni upornosti in frekvenci je enostavno izračunati kapacitivnost kondenzatorja.

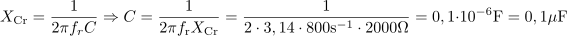Podan zaporedni nihajni krog ima karakteristično oziroma valovno impedanco: Z_C =
2000
Ω.
Valovno impedanco določa razmerje med induktivnostjo tuljave in kapacitivnostjo kondenzatorja.

1. odgovor
2.
3.
4.
5.
6.
7.
8.
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Namig

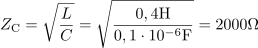dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 36

0

Rešeni primer 36
Izračunaj kapacitivnost kondenzatorja, ki ga vežemo vzporedno tuljavi z induktivnostjo 0,85 H in uporu z upornostjo 1500 Ω, da dobimo nihajni krog z resonančno frekvenco 500 Hz. Kolikšen je tedaj tok, če je vezje priključeno napetost 100 V?
2
Kondenzator, ki zagotovi nihajni krog z resonančno frekvenco 500 Hz, ima kapacitivnost: C =
0.12
μF.
Če uporabimo enačbo, ki določa resonančno frekvenco v vzporednem nihajnem krogu, ugotovimo, da poleg znane frekvence poznamo tudi induktivnost tuljave, ne poznamo pa kapacitivnosti kondenzatorja, ki ustvari nihajni krog.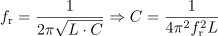

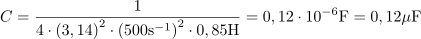Resonančni tok, ki teče iz generatorja v vezje je: I_r =
67
mA.
Ko je vzporedni nihajni krog v resonanci, sta toka skozi tuljavo in kondenzator enaka po velikosti, zato tok iz generatorja v vezje določa le upornost nihajnega kroga.

1. odgovor
2.
0
0
0
0

Namig

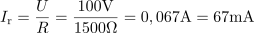dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 37

0

Rešeni primer 37
Izračunaj frekvenco, pri kateri ima vzporedna vezava kondenzatorja s kapacitivnostjo 0,3 μF, upora z upornostjo 1,5 kΩ in tuljave z induktivnostjo 0,2 H maksimalno upornost. Kolikšna je ta upornost?
2
Največja upornost vezja je ob resonančni frekvenci in znaša: R =
1.5
kΩ
Vzporedna vezava kondenzatorja, tuljave in upora predstavlja vzporedni nihajni krog. Pri resonančni frekvenci kapacitivna in induktivna veja ne prispevata k prevodnosti vezja. Admitanca kroga je kar enaka ohmski prevodnosti. Admitanca kroga je v tem primeru najmanjša, impedanca kroga oziroma upornost pa največja.
Z_m = R = 1,5 kΩ
Nihajni krog je v resonanci pri frekvenci: f_r =
650
Hz.
Ker poznamo vse elemente vzporednega nihajnega kroga, lahko izračunamo tudi resonančno frekvenco.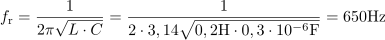

1. odgovor
2.
0
0
0
0

Namig

dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 38

0

Rešeni primer 38
Več električnim motorjem s skupno močjo 45,6 kW želimo izboljšati faktor moči z vrednosti 0,6 na vrednost 0,95. Izračunaj kapacitivnost kondenzatorske baterije za kompenzacijo. Napajalna napetost motorjev je 380 V.
6
Vezava motorjev ima navidezno moč: S =
76
kVA.
Preden se lotimo kompenzacije, nas zanima navidezna moč vezave motorjev.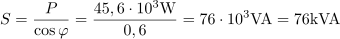

Induktivna jalova moč motorjev pred kompenzacijo je: Q_L =
60.8
kvar.
Za izvedbo kompenzacije potrebujemo še podatek o jalovi moči pred in po kompenzaciji.

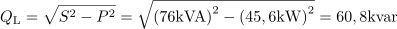Navidezna moč vezave motorjev po kompenzaciji je: S_K =
48
kVA.
Izračunamo še jalovo moč, ki jo pričakujemo po izvedeni kompenzaciji. Do nje pridemo preko navidezne moči po kompenzaciji, ki je določena z delovno močjo in novim faktorjem moči.

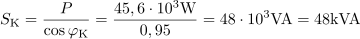Nekompenzirana jalova moč vezave motorjev po izvedeni kompenzaciji je: Q_LK =
15
kvar.
Iz geometrične razlike navidezne moči po kompenzaciji in delovne moči izračunamo preostalo nekompenzirano induktivno jalovo moč.

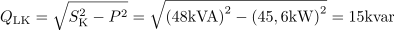Induktivna jalova moč, ki jo je potrebno kompenzirati, je: Q_C =
45.8
kvar.
Razlika med jalovo močjo pred kompenzacijo in jalovo močjo po kompenzaciji predstavlja jalovo moč, ki jo kompenziramo s kondenzatorsko baterijo.

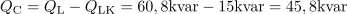Kompenzacijo vezave elektromotorjev, ki izboljša faktor moči iz 0,6 na 0,95, izvedemo s kondenzatorsko baterijo, ki ima kapacitivnost: C =
1
mF.
Jalovo moč kompenziramo s kapacitivnostjo kondenzatorjev pri podani frekvenci. Iz enačbe, ki povezuje kapacitivno jalovo moč, kapacitivnost in frekvenco izračunamo kapacitivnost, ki jo iščemo.

1. odgovor
2.
3.
4.
5.
6.
0
0
0
0
0
0
0
0
0
0
0
0

Namig

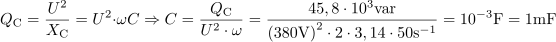dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 39

0

Rešeni primer 39
Trifazni elektromotor z delovno močjo 10 kW, napetostjo 380 V in faktorjem moči 0,8 kompenziramo s kondenzatorsko baterijo jalove moči 5 kvar. Določi faktor moči, ki ga ima vezava po izvedeni kompenzaciji. Izračunaj tok pred kompenzacijo in po njej.
7
Navidezna moč pred kompenzacijo znaša: S =
12.5
kVA.
Za izračun toka pred kompenzacijo potrebujemo navidezno moč pred kompenzacijo, ki jo določimo iz podatkov za delovno moč in faktor moči.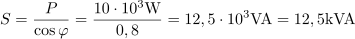

Tok, ki napaja trifazni elektromotor pred kompenzacijo, je: I =
19
A.
Poznavanje velikosti navidezne moči in napajalne napetosti omogoča določitev toka, ki napaja trifazni elektromotor.

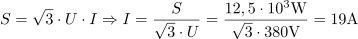Pred izvedbo kompencacije je induktivna jalova moč trifaznega elektromotorja: Q_L =
7.5
kvar.
Na osnovi navidezne in delovne moči lahko izračunamo jalovo moč pred kompenzacijo.

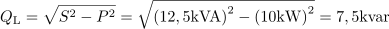Jalova moč, ki ostane nekompenzirana, znaša: Q_LK =
2.5
kvar.
S kompenzacijo se jalova moč zmanjša za 5 kvar, zato lahko izračunamo, kolikšna je po kompenzaciji.

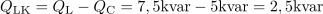Navidezna moč po izvedeni kompenzaciji elektromotorja je: S_K =
10.3
kVA.
Sedaj, ko poznamo tako delovno kot jalovo moč po kompenzaciji, lahko izračunamo tudi končno navidezno moč, iz katere bomo določili tudi tok za napajanje elektromotorja po kompenzaciji.

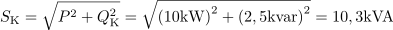Napajalni tok trifaznega kompenziranega elektromotorja je: I_K =
15.7
A.
Z upoštevanjem navidezne moči in napajalne napetosti kompenziranega trifaznega elektromotorja lahko določimo napajalni tok.

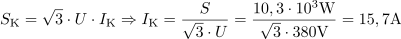Faktor moči se je pri kompenziranem trifaznem elektromotorju bistveno izboljšal in znaša: cosφ =
0.97
.
Tudi za izračun faktorja moči po izvedeni kompenzaciji imamo na razpolago vse potrebne podatke, to je navidezno in delovno moč.

1. odgovor
2.
3.
4.
5.
6.
7.
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Namig

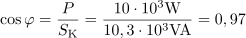dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 40

0

Rešeni primer 40
Kondenzator s kapacitivnostjo 2 μF priključimo preko upora z upornostjo 300 Ω na enosmerno napetost 24 V. Izračunaj vrednost napetosti na kondenzatorju 1,5 ms po vklopu stikala. Izračunaj tudi, kolikšen je takrat tok.
4
Časovna konstanta vezja je: τ =
0.6
ms.
Pred izračunom napetosti in toka določimo časovno konstanto vezja, ki jo določata upornost vezja in kapacitivnost kondenzatorja.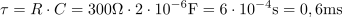

V času 1,5 ms po vklopu stikala je napetost na kondenzatorju že: u_C =
22
V.
Po vklopu stikala narašča napetost na kondenzatorju po eksponentni funkciji. Napetost na kondenzatorju lahko določimo po času 1,5 ms od vklopa stikala, če poznamo časovno konstanto vezja in maksimalno napetost.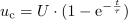

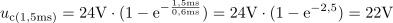Upor omejuje maksimalni tok na vrednost: I =
0.08
A.
Zanima nas tudi maksimalni tok, ki steče takoj ob vklopu stikala in ga omejuje ohmski upor. Izračunamo ga po Ohmovem zakonu.

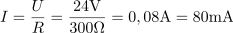Tok v električnem krogu upade 1,5 ms po vklopu stikala na vrednost: i_C =
6.6
mA.
Tok skozi vezje se tako kot napetost spreminja po eksponentni funkciji, le da za razliko od napetosti tok s časom upada. Časovna konstanta pa je enaka za obe veličini, tok in napetost.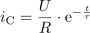

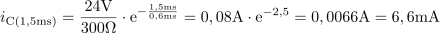1. odgovor
2.
3.
4.
0
0
0
0
0
0
0
0

Namig

dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 41

0

Rešeni primer 41
Kondenzator priključimo na enosmerno napetost 10 V preko ohmske upornosti 2 kΩ. Napetost na kondenzatorju doseže maksimalno vrednost v času 10 ms. Kolikšna je kapacitivnost kondenzatorja? Kolikšna je vrednost napetosti na kondenzatorju 2 ms po vklopu?
3
Časovna konstanta vezja je: τ =
2
ms.
Iz podatka o času polnjenja lahko izračunamo časovno konstanto vezja, saj smatramo, da je kondenzator poln, ko preteče čas v trajanju petih časovnih konstant.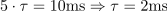

Kondenzator, ki določa časovno konstanto vezja, ima kapacitivnost: C =
1
μF.
Ker je časovna konstanta, ki jo že poznamo, določena z upornostjo in kapacitivnostjo vezja, lahko iz te povezave izračunamo neznano kapacitivnost.

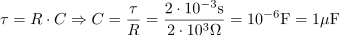dveh milisekundah po vklopu naraste napetost na kondenzatorju iz 0 V na: u_C =
6.3
V.
Zanima nas, kolikšna bo napetost na kondenzatorju 2 ms po vklopu. Ker je časovna konstanta vezja tudi 2 ms, to pomeni, da nas zanima napetost po preteku časa določenega s časovno konstanto. Po definiciji časovna konstanta predstavlja čas, v katerem napetost na kondenzatorju naraste na 63 % končne vrednosti.

1. odgovor
2.
3.
0
0
0
0
0
0

Namig

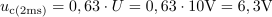dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 42

0

Rešeni primer 42
Izračunaj tok v ničelnem vodniku trifaznega sistema v zvezdni vezavi, za katero poznamo naslednje veličine Z₁ = 20 Ω, cosφ₁ = 0,866, Z₂ = 40 Ω, cosφ2 = 0,71, Z₃ = 11 Ω, cosφ₃ = 0,98.
4
Tok v prvem linijskem vodniku zapišemo s kompleksorjem v obliki: I₁ =
0
A.
Ker je tok v ničelnem vodniku vsota vseh treh linijskih tokov, izračunamo vsakega od njih. Najprej določimo fazni kot, izračunamo maksimalno vrednost toka po Ohmovem zakonu, nato pa še realno in imaginarno komponento toka.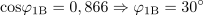

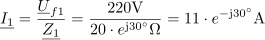
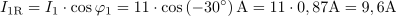
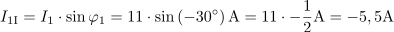
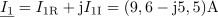Tok v drugem linijskem vodniku zapišemo s kompleksorjem kot: I₂ =
0
A.
Tudi tok v drugem linijskem vodniku L₂ izračunamo na enak način, le da upoštevamo premik napetosti za -120 º glede na L₁.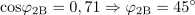

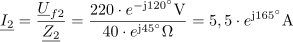
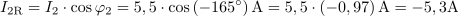
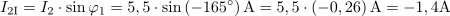
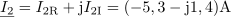V tretjem linijskem vodniku teče tok: I₃ =
0
A.
V tretjem linijskem vodniku je napetost premaknjena za -240 º glede na L₁.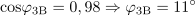

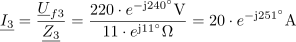
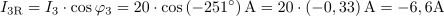
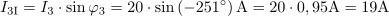
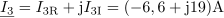V ničelnem vodniku teče tok: I₀ =
0
A.
Tok v ničelnem vodniku predstavlja vsoto vseh treh tokov v linijskih vodnikih.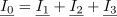

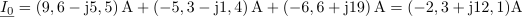1. odgovor
2.
3.
4.
0
0
0
0
0
0
0
0

Namig

dasfasdfasd

Rešitev

asdasfasd
Rešeni primer 43

0

Rešeni primer 43
Za trifazni sistem, vezan v trikot, izračunaj fazne tokove ter celotno delovno moč. Porabnika Z₁₂ in Z₂₃ imata induktivni značaj in faktor moči 0,92, delovna moč vsakega pa je 70 kW. Porabnik Z₃₁ je ohmski in ima delovno moč 30,4 kW. Linijska napetost je 380 V.
5
Tok I₁₂ = 200 A. Jakost toka I₂₃ je: I₂₃ =
200
A.
Ker sta porabnika Z₁₂ in Z₂₃ enaka, enak je njun faktor moči in delovna moč, ki se sprošča na vsakem, lahko sklepamo, da sta tudi toka, ki tečeta skoznju, enaka.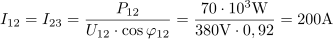

Tokova I₁₂ in I₂₃ zaostajata za pripadajočo napetostjo za fazni kot: φ₁₂ =
23
°.
Fazni kot za tokova I₁₂ in I₂₃ izračunamo iz faktorja moči.

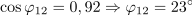Jakost tretjega linijskega toka I₃₁ pa je: I₃₁ =
80
A.
Tudi tok I₃₁ izračunamo iz delovne moči in linijske napetosti z upoštevanjem faktorja moči za breme z ohmskim značajem.

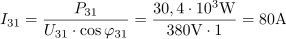Ker je breme Z₃₁ ohmsko, je fazni kot: φ₃₁ =
0
°.
Pri določanju faznega kota upoštevamo, da ima breme Z₃₁ ohmski značaj, zato sta napetost U₃₁ in tok I₃₁v fazi.

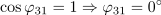Celotna delovna moč vezave je: P =
170.4
kW.
Celotna delovna moč vezave je enaka vsoti vseh delovnih moči, saj se moči medsebojno seštevajo.

1. odgovor
2.
3.
4.
5.
0
0
0
0
0
0
0
0
0
0

Namig

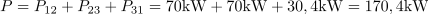dasfasdfasd

Rešitev

asdasfasd

@@ Vrstica 1: / Vrstica 1: @@
 <interaktivni>
-<rezultat>1|2|3|4|5|6|7|8|38</rezultat>
+<reseni>1|2|3|4|5|6|7|8|9|10|11|12|13|14|15|16|17|18|19|20|21|22|23|24|25|26|27|28|29|30|31|32|33|34|35|36|37|38|39|40|41|42|43</reseni>
-<reseni>1|2|3|4|8|9</reseni>
 </interaktivni>
-<animacija>eele_animacija_001_transformator.swf</animacija>
-<animacija>Eele_animacija_002_RLC_vezje_zaporedno_toki_napetosti.swf</animacija>

Test

Iz e-ELEKTROTEHNIKA plus

Redakcija: 19:34, 31. avgust 2010

Preizkusi znanje

Osebna orodja

Navigacija

Iskanje