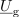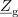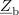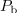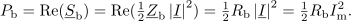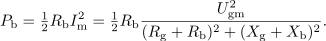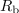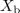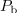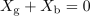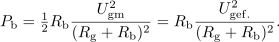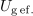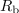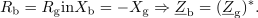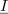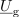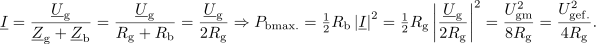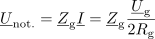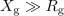Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
Redakcija: 16:09, 14. maj 2010
Slika:OET2 a poglavje 38 slika 05.svgBreme spremenljive impedance je priključeno na realen izmenični vir; sprašujemo se po primerni vrednosti impedance bremena, da bo delovna moč v njem največja.
Pojem prilagoditve smo obdelali že pri enosmernih vezjih, ob vprašanju: kolikšna naj bo upornost bremena, ki ga priključimo na realen vir, da bo moč v bremenu maksimalna. Ugotovili smo, da je tolikšna takrat, ko je upornost bremena enaka nadomestni notranji upornosti vira.
In kako je s to rečjo v izmeničnem vezju? Imejmo nek realen harmonični vir z določeno nadomestno notranjo impedanco. Modelno vezje takšnega vira oblikuje npr. zaporedna vezava neodvisnega napetostnega vira, ki mu pripada kazalec
, in pasivnega dvopola, katerega impedanca
ustreza nadomestni notranji impedanci vira. Na vir priključimo kompleksno breme (slika 5) in se vprašajmo kolikšna naj bo impedanca
bremena, da bo delovna moč
v njem maksimalna? Aktivna moč je določena z realnim delom kazalca moči:
Amplitudo toka določa kvocient amplitude napetosti neodvisnega vira in absolutne vrednosti vsote notranje impedance in impedance bremena:
Naša naloga je najti takšna
in
, da bo moč
maksimalna. Imenovalec ulomka bo kar najmanjši, aktivna moč pa kar največja, ko bo vsota reaktanc bremena in notranjega elementa enaka nič; to je
pri
je
Izraz spominja na enosmerno vezje: kot da bi na enosmerni vir z napetostjo odprtih sponk;
in notranjo upornostjo
priključili breme z upornostjo
in se vprašali po moči v bremenu. Ker pa odgovor od tam že poznamo (da je moč v bremenu maksimalna, ko je njegova upornost enaka notranji), sledi: aktivna moč v kompleksnem bremenu je maksimalna takrat, ko je rezistanca bremena enaka rezistanci notranjega elementa in ko je hkrati tudi reaktanca bremena enaka negativni reaktanci notranjega elementa:
Odgovor je tu: delovna moč v kompleksnem bremenu je maksimalna takrat, ko je impedanca bremena enaka konjugirani notranji impedanci vira. Takrat pravimo, da je kompleksno breme prilagojeno na realen harmonični vir.
V primeru prilagoditve je kazalec
toka skozi breme sofazen s kazalcem
napetosti vira in tudi izraz za maksimalno moč v bremenu je sila preprost:
Zanimiva sta tudi kazalca napetosti na notranjem elementu in na bremenu:
in
Ob prilagoditvi oblikujeta kazalca delnih napetosti s kazalcem napetosti vira enakokrak trikotnik, preseneča pa to, da sta v primeru
kraka tega trikotnika zelo dolga, da je absolutna vrednost kazalca napetosti na bremenu takrat celo nekajkrat večja od absolutne vrednosti kazalca napetosti odprtih sponk; spet nekaj, česar v enosmernih razmerah nismo srečali (slika 6).