Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
| (One intermediate revision not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
| - | Funkcijo <latex>G(t)</latex> smo definirali in poznamo njene lastnosti, ostaja pa še naloga, kako do nje priti, kako jo najti | + | Funkcijo <latex>G(t)</latex> smo definirali in poznamo njene lastnosti, ostaja pa še naloga, kako do nje priti, kako jo najti. Iskanje začnimo s funkcijo <latex>F</latex>, od katere zahtevamo, da zadošča enačbi |
| Vrstica 5: | Vrstica 5: | ||
| - | Z združitvijo te s podobno za ''G'' sledi: | + | Z združitvijo le-te s podobno za ''G'' sledi: |
| Vrstica 11: | Vrstica 11: | ||
| - | Odvod razlike funkcij je enak nič | + | Odvod razlike funkcij je enak nič, ker pa je odvod konstante tudi enak nič, se zgornji funkciji razlikujeta kvečjemu za konstanto, npr. za konstanto <latex>C_0</latex>: |
| Vrstica 29: | Vrstica 29: | ||
| - | Pridevnik »nedoločen« stoji zato, ker se funkcija ''F'' od funkcije ''G'', od funkcije zgornje meje določenega integrala, razlikuje za aditivno konstanto. Zapis ''F''(''t'') = ∫''f''(''t'')d''t'' bi | + | Pridevnik »nedoločen« stoji zato, ker se funkcija ''F'' od funkcije ''G'', od funkcije zgornje meje določenega integrala, razlikuje za aditivno konstanto. Zapis ''F''(''t'') = ∫''f''(''t'')d''t'' bi lahko razumeli tudi kot nekakšno nedoločeno vsoto paketov ''f''(''t'')d''t'', kateri bi mogli brez škode prišteli poljubno konstanto. Nadalje vidimo, da je iskanje nedoločenega integrala ''F'' funkcije ''f'' opravilo, ki je obratno odvajanju: iskanje funkcije ''F'' ustreza iskanju tiste funkcije, katere odvod je funkcija ''f''. |
{{Hierarchy footer}} | {{Hierarchy footer}} | ||
Trenutna redakcija s časom 09:30, 8. junij 2010
Funkcijo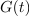
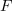
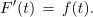
Z združitvijo le-te s podobno za G sledi:
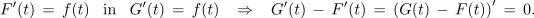
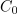
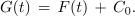
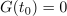
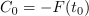
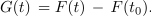
Funkciji F, ki zadošča enačbi F′ = f, rečemo nedoločen integral funkcije f; to zapisujemo v naslednjih enakovrednih oblikah:
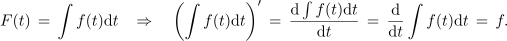
Pridevnik »nedoločen« stoji zato, ker se funkcija F od funkcije G, od funkcije zgornje meje določenega integrala, razlikuje za aditivno konstanto. Zapis F(t) = ∫f(t)dt bi lahko razumeli tudi kot nekakšno nedoločeno vsoto paketov f(t)dt, kateri bi mogli brez škode prišteli poljubno konstanto. Nadalje vidimo, da je iskanje nedoločenega integrala F funkcije f opravilo, ki je obratno odvajanju: iskanje funkcije F ustreza iskanju tiste funkcije, katere odvod je funkcija f.
 5.4.2 Odvod funkcije zgornje meje določenega integrala
| 5.6 Zveza med določenim in nedoločenim integralom
|
